Инженерами АО «ЦИФРА» выполнена серия вычислительных краш-тестов автомобильного рамного прицепа, в результате чего определены характеристики энергопоглощения прицепа, а также его деформированное состояние при наезде на него движущегося транспорта при различных скоростях.
Вебинар: Научно-техническое сопровождение проектирования особо опасных и технически сложных промышленных объектов
Приглашаем на открытый вебинар, посвящённый актуальным вопросам проведения научно-технического сопровождения проектирования (НТС).
Помимо своего основного предназначения – перевозки различных грузов в составе с транспортным средством (ТС), прицепы применяются и в других целях. В частности, легковые прицепы часто используются дорожно-ремонтными службами как временное ограждение на оживленных участках дорог, на котором проводятся ремонтные или эксплуатационные работы (см. рис. 1).
Рисунок 1 – Прицеп прикрытия при проведении дорожно-ремонтных работ
Для оценки эффективности применения таких прицепов в качестве временных заграждений с точки зрения безопасности как работников дорожно-ремонтных служб, так и участников дорожного движения, необходимо выполнять анализ возможных аварийных ситуаций при столкновении прицепа и движущегося транспорта. Поскольку натурные краш-тесты, как правило, дорогостоящи и требуют значительного времени, на сегодняшний день подобные задачи решаются при помощи конечно-элементного моделирования. Инженерами АО «ЦИФРА» решена серия модельных задач наезда транспортного средства на прицеп, выполнен анализ поглощения кинетической энергии при ударе и развития пластических деформаций в элементах прицепа. Расчеты выполнены в наиболее консервативной постановке, при которой вся кинетическая энергия движущегося ТС преобразуется в энергию деформации прицепа, а само ТС является недеформируемым.
Моделирование краш-тестов обычно сопряжено с высокими скоростями, большими перемещениями и поворотами, развитой физической нелинейностью и сложным контактным взаимодействием. На сегодняшний день наиболее передовым и популярным инструментом для решения высоконелинейных динамических задач является код Ansys/LS-DYNA, реализующий метод конечных элементов. Решение выполняется методом прямого интегрирования уравнений движения по явной центрально-разностной схеме.
Постановка задачи
Геометрия
Рассматривается одноосный легковой прицеп рамной конструкции, в передней части которого расположено сцепное устройство, а в задней – бампер (см. рис. 2).
Рисунок 2 – Геометрическая модель несущего остова прицепа
Основные несущие элементы выполнены из квадратной трубы 150х150 мм с толщиной стенки 4-5 мм и соединяются между собой при помощи сварки и болтов. Все элементы конструкции прицепа выполнены из высокопрочной стали с пределом текучести 600 МПа.
Конечно-элементная модель
Движущееся транспортное средство, которое совершает наезд на прицеп, представлено как идеальная недеформируемая плоская стена массой 1.67 т, движущаяся по нормали к прицепу со стороны бампера. Рассматривается три удара с различной начальной скоростью: 10 м/с (36 км/ч), 20 м/с (72 км/ч) и 30 м/с (108 км/ч). Транспортное средство, стоящее перед прицепом, моделируется как неподвижное абсолютно твердое тело (*RIGIDWALL_PLANAR). Сцепление с ним моделируется как граничное условие запрета всех трансляционных степеней свободы. Контактное взаимодействие между абсолютно твердыми телами (АТТ) и прицепом, а также контакт отдельных элементов прицепа между собой при больших деформациях обеспечивается благодаря автоматическому контактному алгоритму *CONTACT_AUTOMATIC_SINGLE_SURFACE (см. рис. 3).
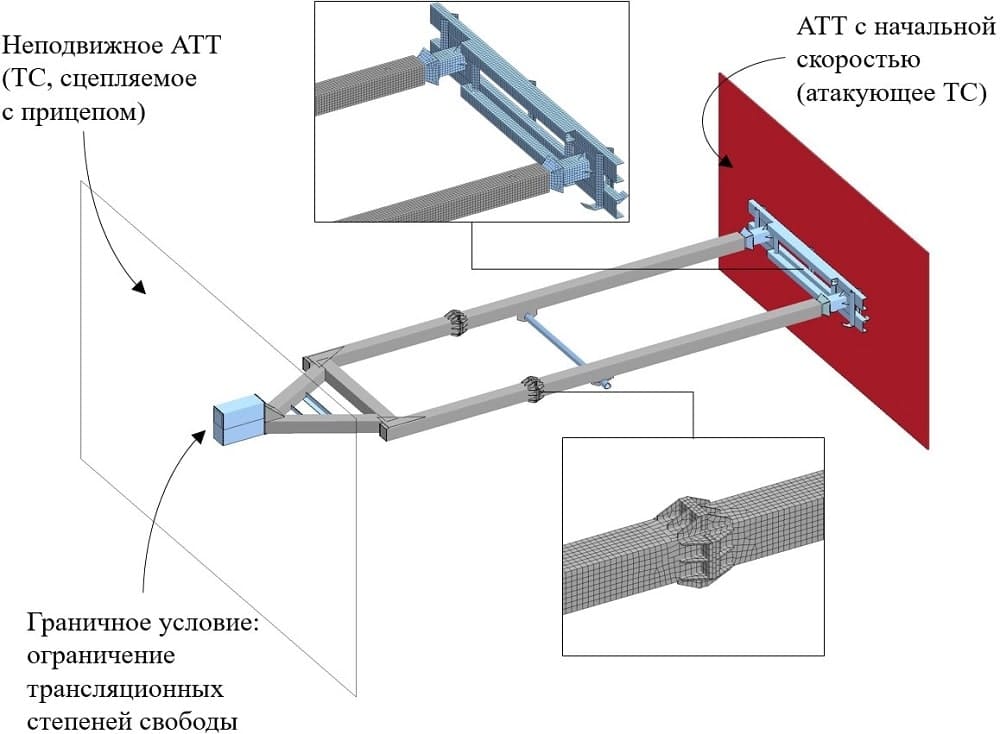
Рисунок 3 – Постановка задачи фронтального краш-теста прицепа
Для подготовки конечно-элементной сетки был использован автоматический сеточный генератор Ansys Meshing. Все элементы прицепа аппроксимируются полноинтегрируемыми оболочечными конечными элементами (*SECTION_SHELL ELFORM=16). Из модели исключены некоторые конструктивные элементы, несущественные с точки зрения расчета. Сварные соединения моделируются «склеенным» контактом (*CONTACT_TIED_SURFACE_TO_SURFACE) либо объединением конечно-элементных сеток, болтовые – заменой болтов на абсолютно твердые тела-связи (*CONSTRAINED_NODAL_RIGID_BODY) и заданием контактного взаимодействия.
Краш-тесты характеризуются высокими скоростями деформаций и значительными пластическими деформациями, поэтому для описания физических соотношений была выбрана модель Купера-Саймондса (*MAT_PIECEWISE_LINEAR_PLASTICITY). Данная модель основана на критерии текучести Мизеса и учитывает влияние скорости деформаций в материале на его прочностные характеристики.
Результаты
Поскольку предназначение прицепа – ограждение зоны проведения дорожно-ремонтных работ и обеспечение безопасности работников, то его эффективность определяется способностью поглотить кинетическую энергию движущегося ТС, деформируясь.
Согласно одному из фундаментальных законов физики, полная энергия в замкнутой системе должна оставаться постоянной. Однако, численное решение задачи вносит некоторую ошибку в энергетический баланс системы в виде паразитной энергии (hourglass energy), накапливающейся из-за нефизичного деформирования конечно-элементной сетки. Поэтому в ходе решения задачи важно следить, чтобы величина паразитной энергии была несопоставимо меньше энергии деформации в системе и не могла повлиять на результаты расчета.
В результате моделирования краш-теста в данной постановке установлено, что прицеп во всех случаях оказывается способен поглотить всю кинетическую энергию ТС, с которым он сталкивается. При этом различная скорость удара оказывает влияние на характер деформирования и скорость поглощения кинетической энергии. Рассмотрим каждый расчетный случай подробнее.
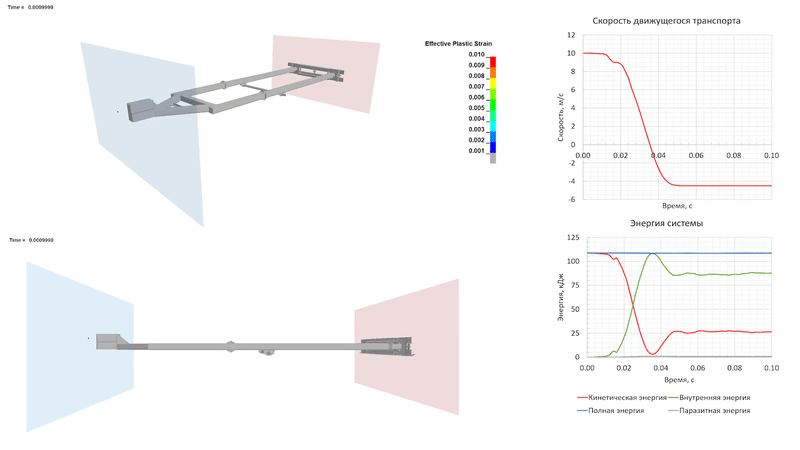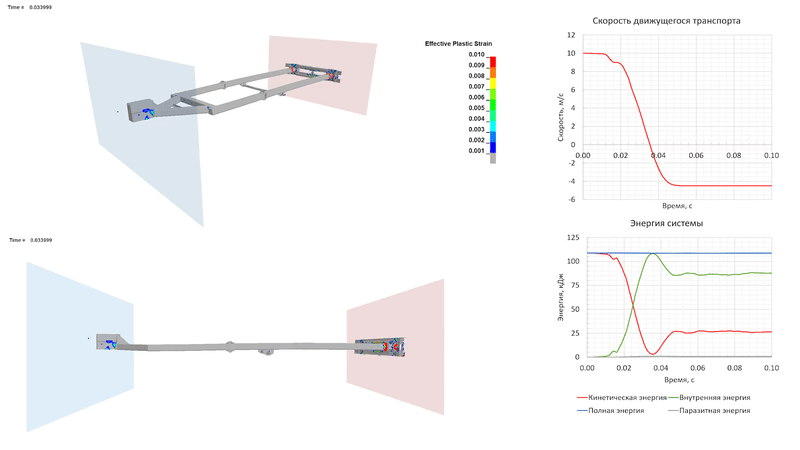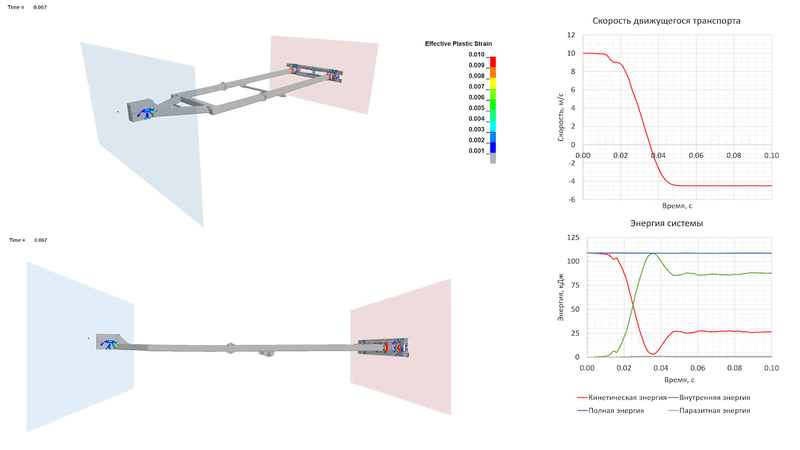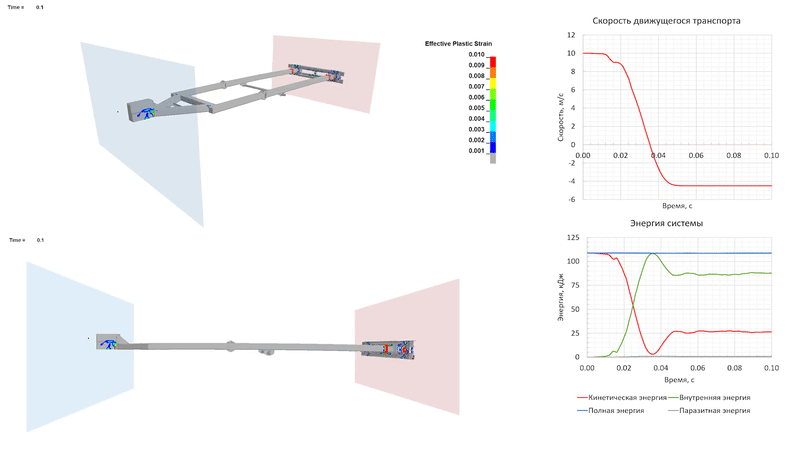
Удар на скорости 10 м/с (36 км/ч)
В случае столкновения на скорости 10 м/с рама прицепа деформируется практически полностью упруго, за исключением локальных зон развития пластических деформаций. К 0.037 с расчета движущееся ТС останавливается, а его кинетическая энергия полностью преобразуется в энергию деформации конструкции прицепа. Энергия упругой деформации создает пружинящее действие, за счет которого движущееся ТС отскакивает назад.
Удар на скорости 20 м/с (72 км/ч)
При столкновении на скорости 20 м/с возникают значительные неупругие деформации в области сцепления со стоящим впереди ТС, а также в болтовых и сварных соединениях бампера. Кинетическая энергия движущегося ТС полностью поглощается конструкцией прицепа к 0.045 с расчета. Из-за необратимых деформаций упругого отскока не происходит.
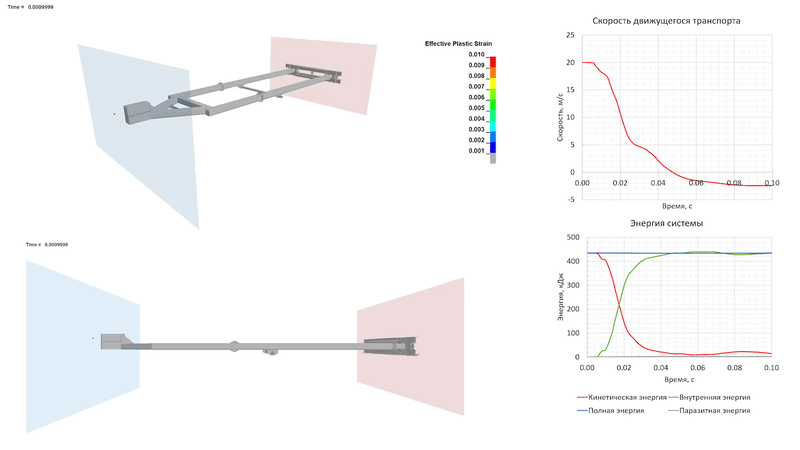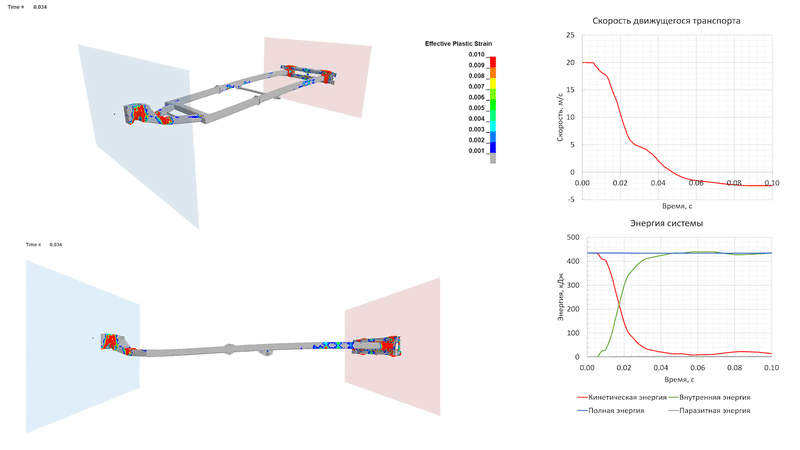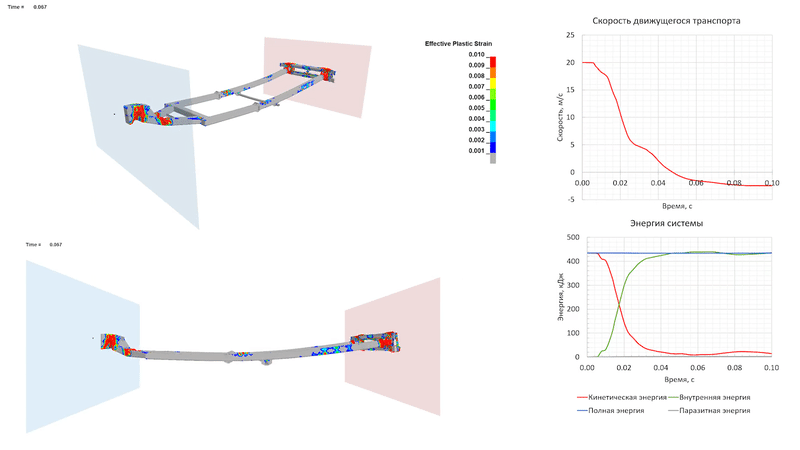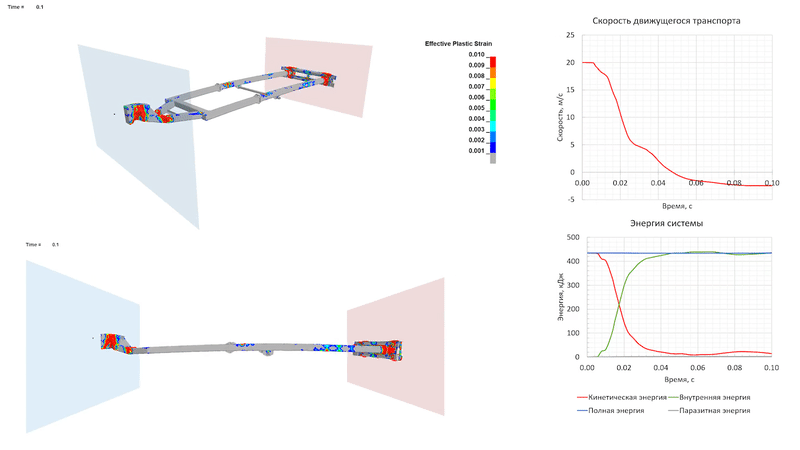
Удар на скорости 30 м/с (108 км/ч)
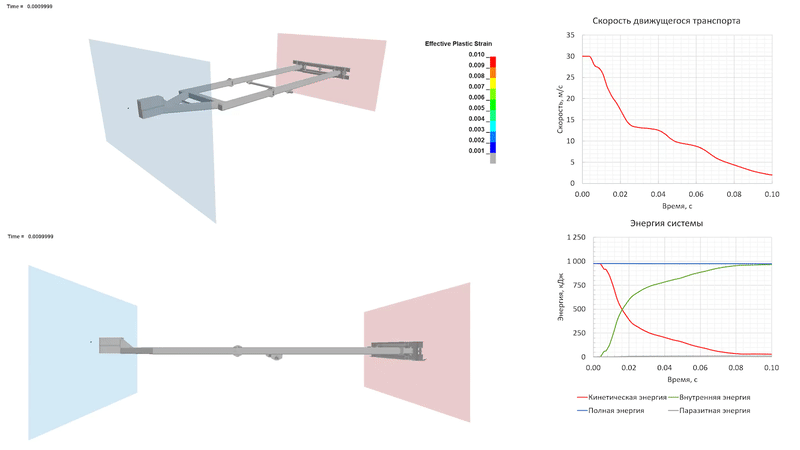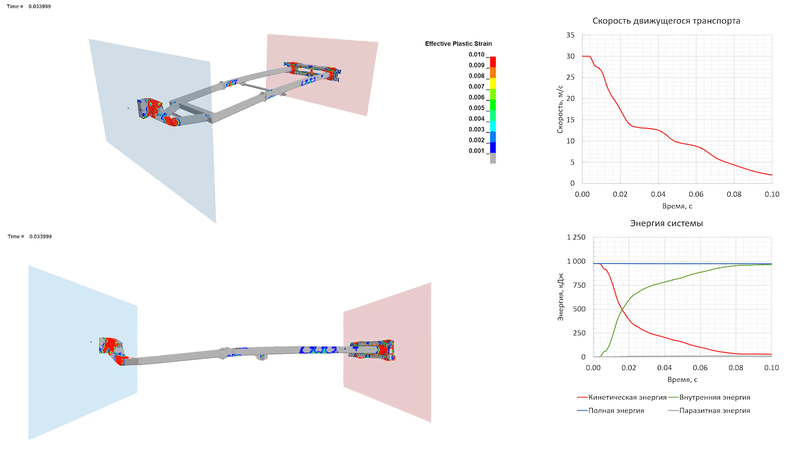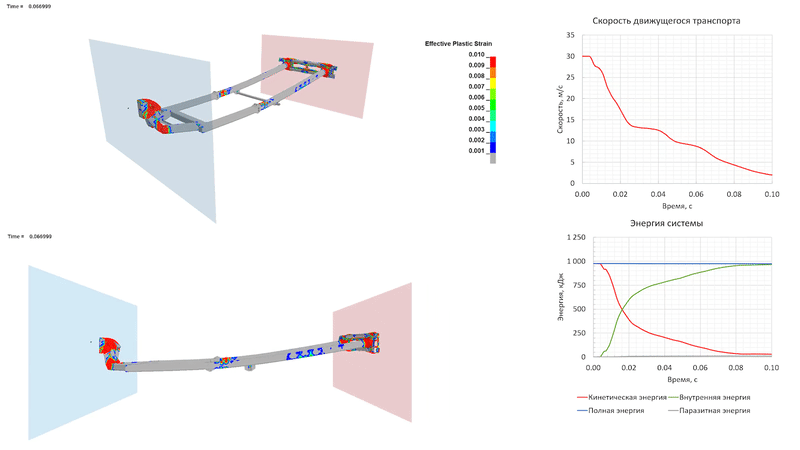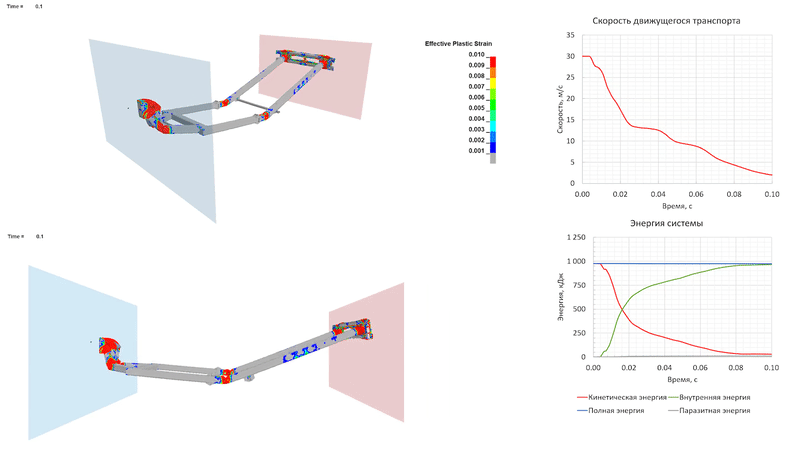
При столкновении на скорости 30 м/с пластические деформации развиваются также в средней части продольных элементов рамы прицепа, за счет чего прицеп начинает «складываться». Движущееся ТС полностью останавливается к 0.1 с процесса, преобразуя кинетическую энергию в энергию деформации элементов прицепа. Из-за развитых пластических деформаций упругого отскока, как и в предыдущем случае, не происходит.
Заключение
Столкновение транспортных средств – высокоскоростной динамический процесс, который протекает за считанные доли секунды и характеризуется значительными неупругими деформациями и повреждениями. Математическое моделирование краш-тестов на сегодняшний день обладает высокой предсказательной силой, а также гораздо дешевле физических экспериментов, что в совокупности делает его ключевым инструментом при анализе эффективности проектных решений.
В статье рассмотрена модельная задача наезда движущегося ТС на легковой прицеп, использующийся для временного ограждения при проведении дорожно-ремонтных работ. Различные начальные скорости движущегося ТС оказывают значительное влияние на характер деформирования прицепа; тем не менее, в диапазоне скоростей атаки 10–30 м/с (36–108 км/ч) конструкция прицепа оказывается способна полностью поглотить кинетическую энергию движущегося ТС.
