Вопросы долговечности и ресурса объектов энергетики, таких как турбины, насосы или элементы трубопроводной арматуры, зачастую непосредственно связаны с зарождением и развитием повреждений и трещин в металле изделия. Для прогнозирования ресурса конструкций с трещинами необходимо применять совокупность методов неразрушающего контроля и математического моделирования.

Неразрушающий контроль

Неразрушающий контроль и обследования позволяют определить размер трещин и их расположение в изделии. Эти данные являются входными при математическом моделировании и инженерном анализе распространения трещин.

По ГОСТ 18353-73 методы неразрушающего контроля разделяются на следующие виды:

• Акустический контроль (ультразвуковой метод);
• Магнитный контроль (магнитопорошковая дефектоскопия);
• Контроль проникающими веществами;
• Радиоволновый контроль;
• Радиационный контроль (рентгеновский метод);
• Оптический контроль;
• Тепловой контроль;
• Электрический контроль;
• Электромагнитный (вихретоковый) контроль;
• Твердометрия (измерение твердости).

Разрешающая способность данных методов различна. Если применяемый метод неразрушающего контроля не позволил обнаружить трещины, то в дальнейшем анализе размер трещины принимается равным разрешающей способности метода.

Механика разрушения

Поскольку с позиции линейной теории упругости напряжения в вершине трещины бесконечны (сингулярность), то для оценки напряженного состояния конструкции вблизи конца трещины используют конечные коэффициенты интенсивности напряжений (КИН). Данные параметры определяются методами линейной механики разрушения для заданной геометрии объекта, трещины и условий нагружения.

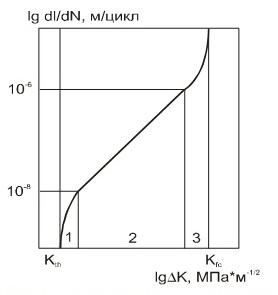
Для анализа распространения усталостной трещины применяется комбинация линейной механики разрушения и усталостной прочности. Анализ усталостного распространения трещины традиционно основывается на законе Пэриса. Данный закон является линейной интерполяцией экспериментальных данных о зависимости приращения длины трещины на цикле нагружения (da/dn) к изменению коэффициента интенсивности напряжений на цикле (∆K). График строится в логарифмическом масштабе. Большинство применяемых на практике конструкционных материалов демонстрируют линейное поведение, отображенное на втором участке графика.

Закон Пэриса может быть записан в следующем виде, где C и m являются константами материала:

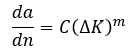
Переписав закон Пэриса можно выразить число циклов ∆n, на котором трещина вырастет на длину ∆a при заданной циклической нагрузке ∆K для материала с параметрами C, m:

Усталостный рост трещины

Таким образом, процедура определения ресурса и долговечности конструкции сводится к нахождению коэффициента интенсивности напряжений для трещины заданной конфигурации. В настоящее время традиционным методом решения этой задачи является метод конечных элементов. С нахождением значения КИН может быть рассчитано число циклов, необходимое для продвижения (распространения) трещины на малую длину, после чего трещина в задаче удлиняется, расчетная сетка перестраивается, проводится новый расчет КИН. Процедура повторяется пока трещина не достигнет критического значения.

Направление развития трещин

Важной задачей при анализе распространения трещин являются определение направления их развития. Направление развития трещины определяется на основе одного из критериев:

• максимальных растягивающих напряжений (Maximum circumferential stress criterion – Erdogan, Sih, 1963);
• максимума скорости освобождения энергии (Maximum energy release rate criterion – Hussain, 1974);
• минимума плотности энергии деформации (Minimum strain energy density factor criterion – Sih, 1974).

Для случая изотропного материала существуют аналитические выражения для углов распространения трещины из вершины, в зависимости от коэффициентов интенсивности напряжений.

Алгоритм расчета КИН для ортотропного слоя более сложен и состоит из следующих этапов: решается характеристическое уравнение 4-го порядка, коэффициентами которого являются компоненты тензора жесткости в локальной системе координат трещины. Комплексные корни этого уравнения входят в коэффициенты системы уравнений 2-го порядка, из которой находятся коэффициенты интенсивности напряжений (M.A. Gregory, C.T. Herakovich. Predicting crack growth direction in unidirectional composites. J. of Composite Materials. Vol. 20, 1986).

Методы расчета распространения трещин в ортотропных материалах могут быть востребованы при расчетах долговечности композитов или деталей, изготовленных на 3D принтере.

Моделирование распространения трещин МКЭ

Моделирование распространения трещины при расчетах методом конечных элементов может быть реализовано различными способами.

Моделирование роста трещин в пластине

1. Наиболее простым, но требующим участия пользователя, является ручное перестроение модели – продление трещины и создание новой расчетной сетки. Данный метод можно автоматизировать с помощью макроса или внешней процедуры.

2. Альтернативным подходом является технология морфинга сетки (mesh morphing), позволяющая двигать узлы и разделять конечные элементы. При работе в ПО ANSYS 17 доступно приложение RBF Morph ACT Extension для быстрой и удобной работы пользователя напрямую с узлами расчетной сетки.

3. Третьим методом является расширенный метод конечных элементов (eXtended Finite Element Method– XFEM), позволяющий искать решения уравнений в частных производных для разрывных функций.  Данный метод дает возможность моделировать рост трещины в произвольном направлении, не зависящем от границ конечных элементов. Основное преимущество XFEMсостоит в том, что нет необходимости перестраивать или сгущать сетку для моделирования роста трещины.