Профилирование — один из ключевых этапов при проектировании и анализе регулирующих устройств. 

Результатом профилирования является расходная характеристика — зависимость пропускной способности системы от степени открытия клапана для постоянного перепада давления. Вместо серийных испытаний для данной задачи может быть применено численное моделирование с параметризацией задачи.

Условия эксплуатации клапана могут быть различными и в некоторых случаях может происходить кавитация — образование пузырьков газообразной фазы в областях низкого давления. Поскольку это ведёт к потерям энергии и потенциальным нежелательным эффектам (например эрозии от лопающихся пузырьков образовавшегося газа как на рисунке 1), нередко требуется определить условия эксплуатации, при которых кавитация не будет происходить. Численное моделирование может быть эффективно применено для определения начала кавитации, поскольку позволяет полностью рассмотреть распределение поля давлений в потоке.

Рисунок 1 – «Кавитационное разрушение: а - крыльчатки насоса; б – трубопровода» [1].

Рабочая среда помимо жидкой фазы нередко может содержать твёрдые вкрапления, также вызывающие эрозию (примеры на рисунке 2). В таком случае важно учесть, как сильно это может влиять на долговечность устройства, то есть определить скорость эрозии частицами примеси. Численное моделирование позволяет получить как качественные, так и количественные характеристики эрозии, в зависимости от объёма имеющихся предварительных данных.

Рисунок 2 – Пример последствий эрозии твёрдыми частицами — «деформация трима дроссельной заслонки» [2].

Для моделирования вышеописанных задач было использовано программное обеспечение Ansys Fluent. В качестве демонстрационного примера рассматривается упрощённая модель шарового клапана с прилегающими к нему с двух сторон трубами (рисунок 3)

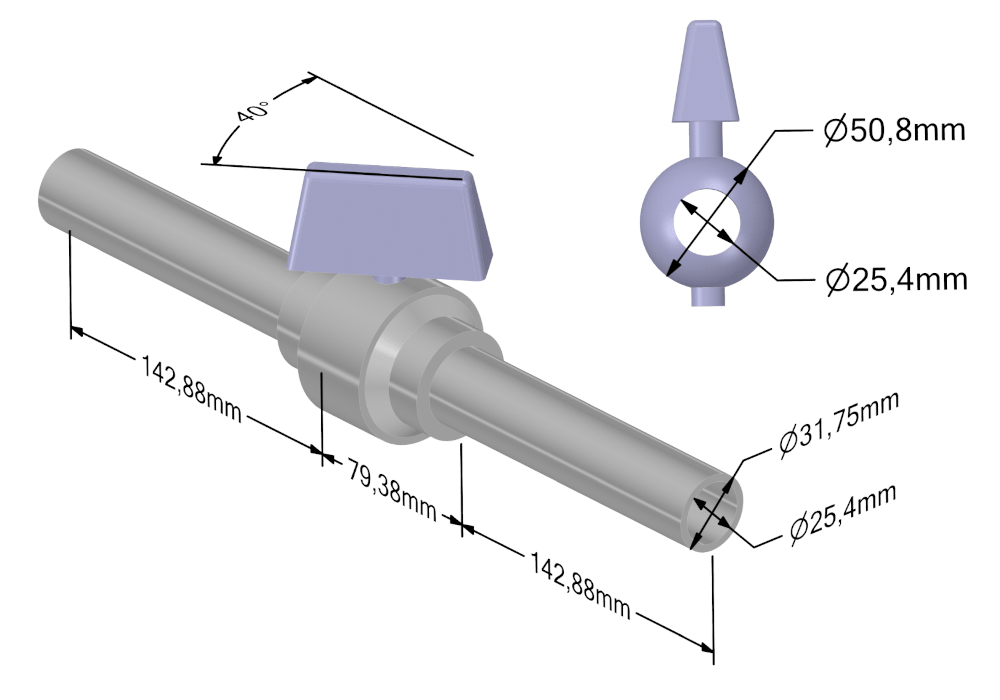Рисунок 3 – Геометрия задачи с указанием основных размеров.

Постановка задачи

Расчётная область представляет собой объём, заполненный рабочей средой (в нашем случае водой при 25℃), при этом область ниже по потоку после клапана обладает большей длинной (рисунок 4). Это необходимо для того, чтобы неоднородности потока, вызванные формой клапана, успевали релаксировать до достижения плоскости выхода и граничное условие на ней — равномерное распределение давления — соответствовало реальной картине процесса. Степень открытия клапана определяется углом поворота вентиля φ: значение φ=40° соответствует минимальному (при шаге 5°) положению, при котором рабочая среда может проходить через клапан (клапан практически закрыт); значение φ=0° соответствует полностью открытому состоянию, и в этом случае расчётная область представляет собой сплошной цилиндр.

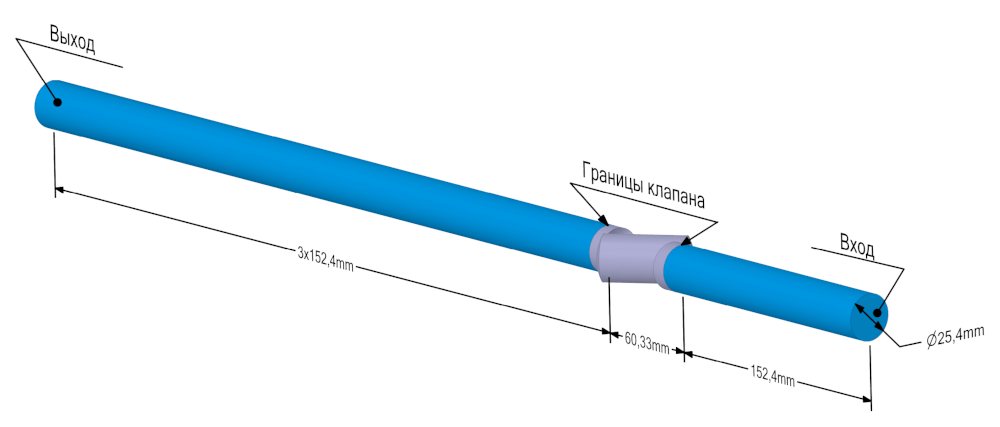Рисунок 4 – Геометрия расчётной области с указанием основных размеров.

Представлен случай для φ=40°.

Граничное условие на выходе – фиксированное давление на всей поверхности. Граничное условие на входе отличается в зависимости от целей расчёта и может представлять собой как фиксированное давление, так и фиксированный расход рабочей среды через поверхность. 

Система подразумевает установившееся турбулентное течение, потому все описанные далее распределения получены в результате расчёта стационарной задачи с применением k-ε модели турбулентности.

Результаты

Расчёты для получения расходной характеристики, продемонстрированной на рисунке 5, представляют собой идентичные действия, повторяемые для каждого исследуемого положения вентиля. Необходимо задать такое давление на входе расчётной области, чтобы перепад давления на границах клапана составлял 1 кгс/(см^2 )≈0.098 Мпа, что является общепринятым значением при профилировании. Таким образом подготавливаются расчётные модели под каждый исследуемый процент открытия клапана (либо используется одна параметризованная модель с возможностью варьирования процента открытия клапана). Результат расчёта каждой модели — расход воды Q при данных условиях, который и определяет расходную характеристику. 

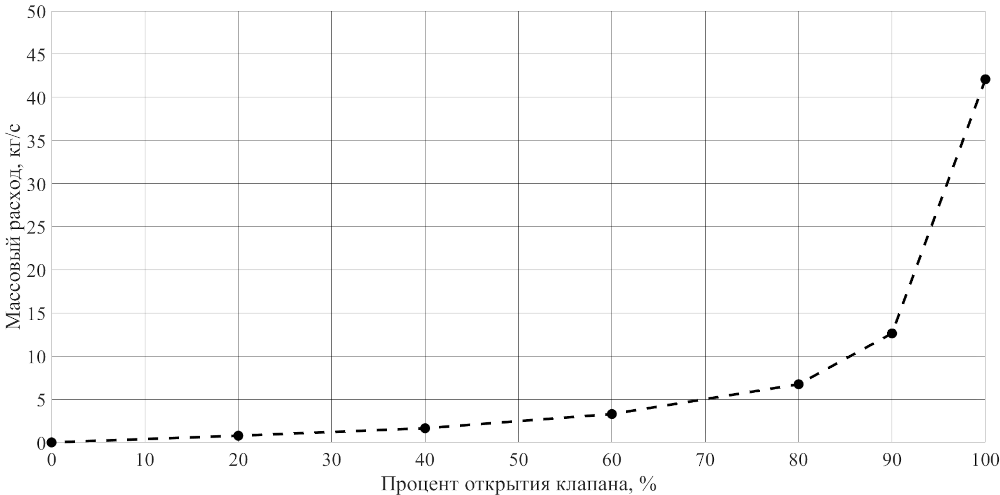Рисунок 5 – Расходная характеристика клапана.

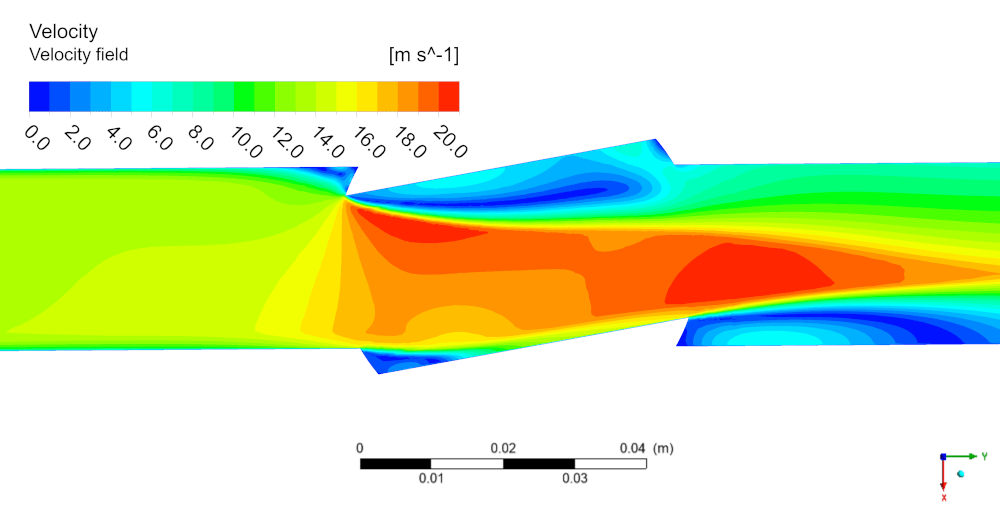
Анализ кавитации и эрозии проведены на примере случая φ=10℃ (клапан открыт на 80%). Характер течения (рисунок 6a) в неполностью открытом клапане располагает к возникновению областей пониженного давления. В частности, если рассматривать центральную плоскость течения, такие области наблюдаются у входа в клапан и после выхода из него (рисунок 6б).

а) 

б) 

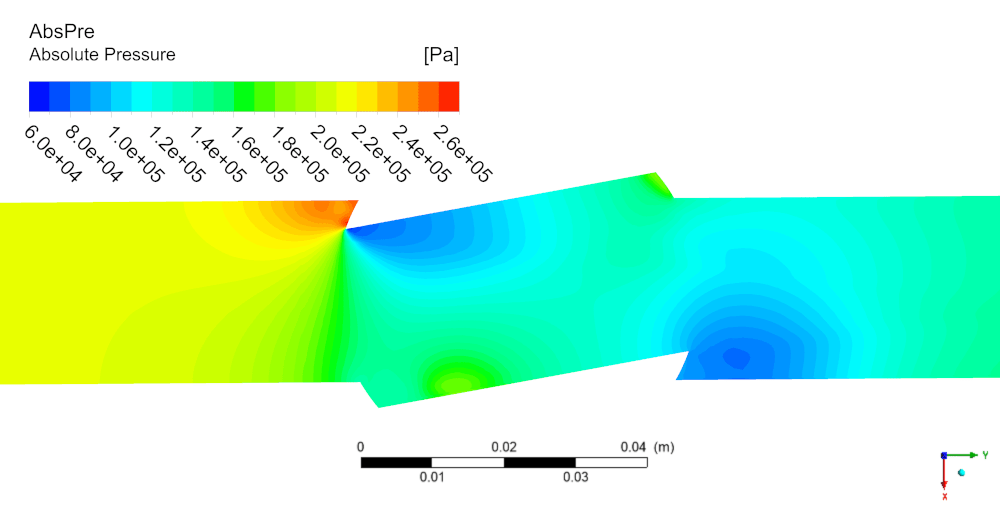
Рисунок 6 – Распределение величин на центральной плоскости клапана для φ=10° и Q=6.74 кг/с: а – поле скорости ν; б – абсолютное давление P_abs.

В ходе расчётов область значений давления ничем не ограничена, однако на практике в случае, если давление опускается до давления насыщенного пара P_(н.п.) вещества рабочей среды (в данном случае P_(н.п.)=3160 Па для воды при 25℃), происходит кавитация – образование пузырьков пара. Для случая Q=6.74 кг/с давление во всём объёме не опускается ниже P_(н.п.), следовательно, кавитация не происходит. Если же рассмотреть большие расходы, то можно явно выделить области P_abs<P_(н.п.) (рисунок 7).

а)

б) 

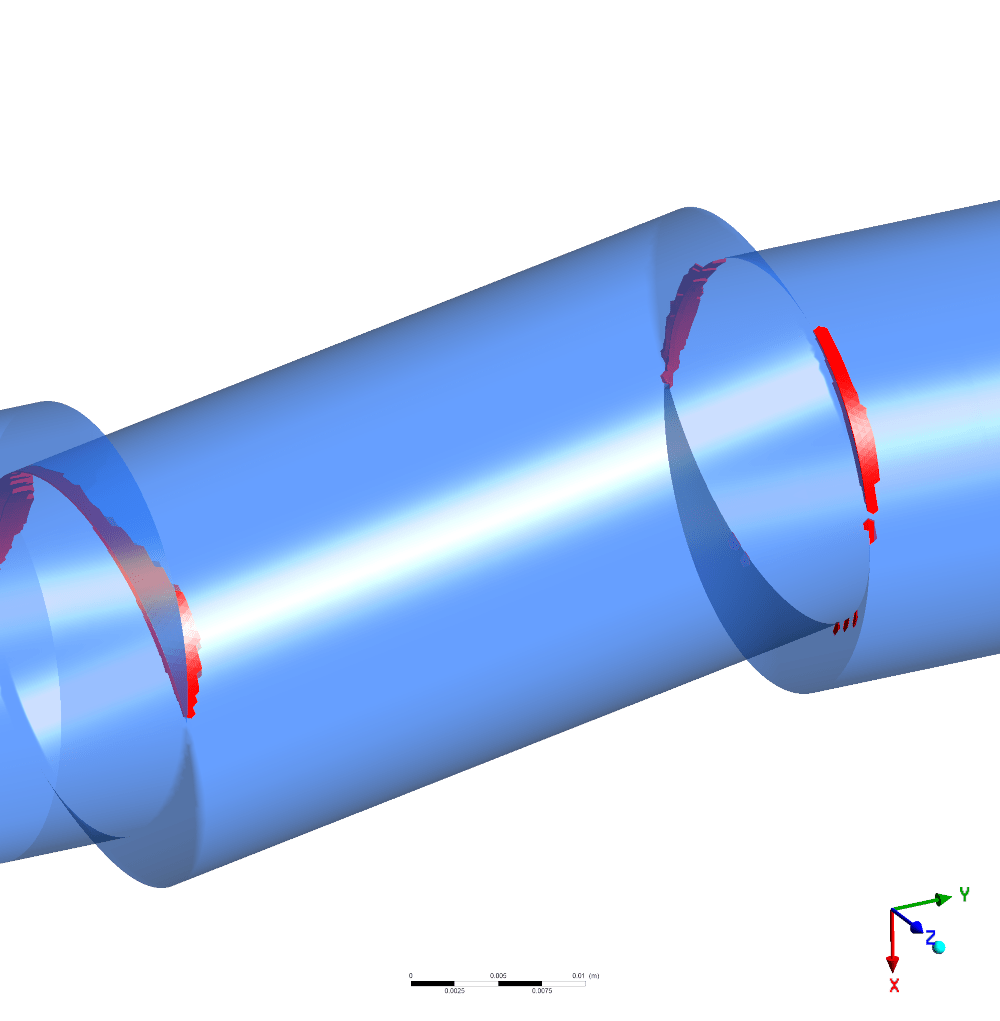
Рисунок 7 – Анализ кавитации. Красным выделены области P_abs<P_(н.п.): а – Q=12 кг/с; б – Q=20 кг/с.

Результаты, представленные на рисунке 7, можно интерпретировать следующим образом — в потоке будет происходить кавитация, поскольку абсолютное давление опускается до давления насыщенного пара в выделенных областях. Таким образом начало кавитации расположено в диапазоне Q∈(6.74 ;12)  кг/с. При необходимости имеется возможность полноценного моделирования потока с учётом кавитации при помощи реализованного в Ansys Fluent метода Cavitation Model.

Возможная эрозия пузырьками газа является одной из причин, из-за которых кавитации стараются избегать. Вышеописанный подход позволяет чётко определить режимы эксплуатации без кавитации. При этом ещё одним источником эрозии могут служить примеси твёрдых частиц (рисунок 8), которые нередко являются неизбежным фактором в работе регулирующих систем.

Рисунок 8 – «Фотографии стальной поверхности после 10-часовой эрозии в растворе, содержащем 50 кг/м3 цезия» [3].

Ansys Fluent обладает широким инструментарием для моделирования многофазных систем. В частности, Discrete Phase Model (DPM), позволяет рассчитывать траектории мелких частиц в рабочей среде, и обладает широким спектром настроек, позволяющих при необходимости:

• учитывать влияние частиц на течение дисперсионной среды;
• учитывать взаимодействие частиц друг с другом;
• задавать несколько сортов частиц, или функцию распределения частиц по размерам;
• учитывать вращение частиц и стохастических характер обтекания частиц жидкостью;
• задавать функцию столкновения частиц со стенками в произвольной форме;
• и т.д.

Далее при помощи полученных данных о скорости, энергии и траектории частиц рассчитывается скорость эрозии стенок, при помощи пользовательской модели эрозии, или же одной/нескольких из встроенных моделей с изменяемыми коэффициентами:

• Finnie Erosion Model — расчёт, в котором эрозийный износ связан с кинетической энергией частиц;
• Oka Erosion Model — расчёт основывается на известном значении скорости эрозии при перпендикулярном ударе частицы о стену;
• McLaury Erosion Model — расчёт берёт за основу пластичность материала;
• и т.д.

В качестве примера рассмотрена эрозия песком, а именно сферическими частицами трёх сортов (диаметры 0.1, 0.5 и 1 мм) с плотностью 1500 кг/м^3. Объёмная доля частиц каждого сорта составляет 5% от объёма втекающей жидкости. Скорость эрозийного износа рассчитана при помощи модели Oka и представлена на рисунке 9.

а)

б)  

в)

г)  

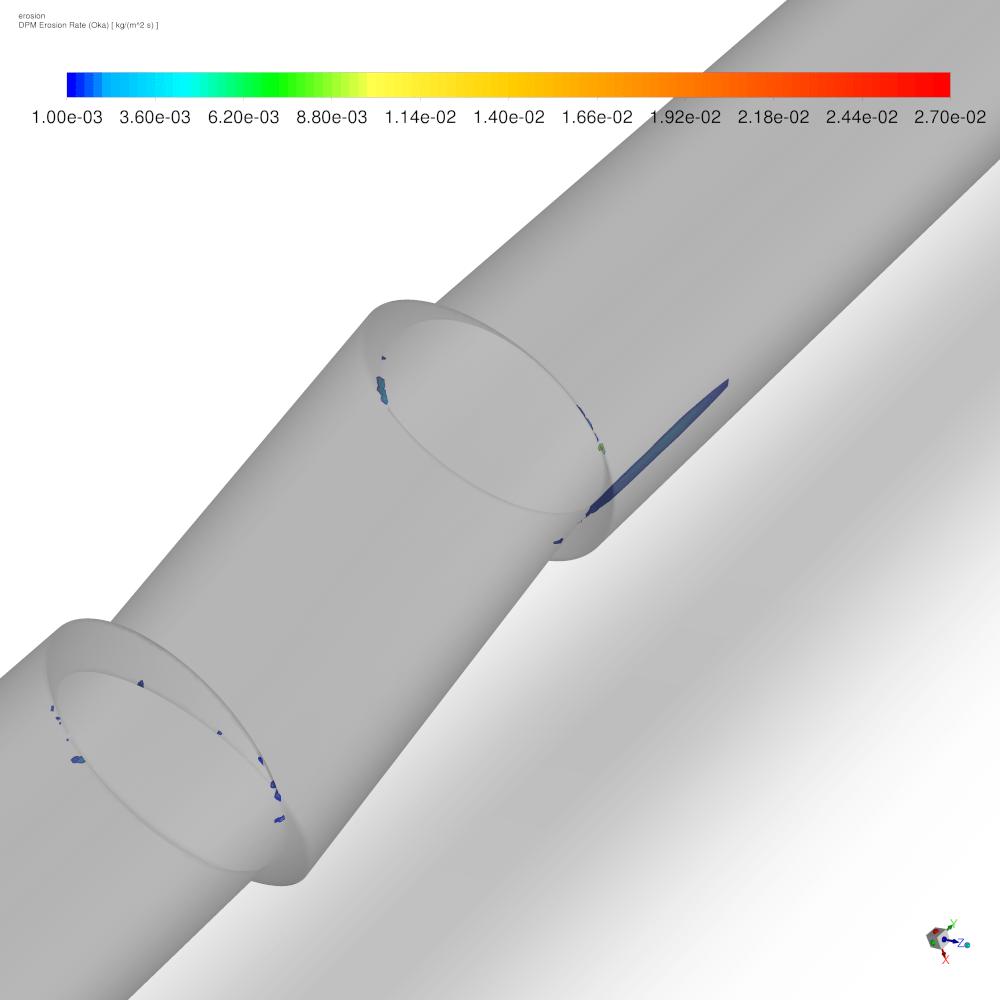
Рисунок 9 – Скорость эрозийного износа: а – суммарная эрозия; б – эрозия частицами 0.1 мм; в – эрозия частицами 0.5 мм; г – эрозия частицами 1 мм.

Можно видеть, что частицы мелкого диаметра способствуют эрозии на выходе из клапана (захватываются областью низкого давления). В то же время более крупные частицы за счёт большей инерции активнее сталкиваются с препятствием на входе в клапан, а также с наклонённой относительно оси стенкой клапана. Как итог, данный подход позволяет качественно прогнозировать области системы, подверженные эрозии, а также выявить вклад отдельных составляющих примеси в общую скорость эрозии.

Количественный анализ эрозии требует основательного выбора модели эрозии и её параметров, для чего в большинстве случаев необходимы экспериментальные данные, полученные для исследуемых материалов и в близких к исследуемым условиях.

Вывод

Можно заключить, что численное моделирование позволяет проводить разносторонний точный анализ регулирующих устройств, требуя меньше временных и финансовых затрат, чем натурные испытания. Опыт, полученный специалистами АО «ЦИФРА» при решении данной задачи, применяется для моделирования систем более сложных форм и нетривиальных условий эксплуатации. 

Список использованных источников

[1] – Масанский, О. А., Казаков, В. С., Токмин, А. М., Свечникова, Л. А., Астафьева, Е. А., 2015. Материаловедение и технологии конструкционных материалов;

[2] – Агазаде, Н. Р., 2023. Контроль песчаной эрозии в дроссельных заслонках. Sciences of Europe # 129.

[3] – Teng, W., Linfeng, J., Qihang, H., Jie, Q., Xinguo, F., 2024. Erosion characteristics of carbon steel in the sand and mud containing solution. International Journal of Electrochemical Science 19.