Специалистами АО «ЦИФРА» осуществлено моделирование распылительной форсунки с использованием гибридной модели VOF-to-DPM.
Форсунка – это устройство с одним или несколькими калиброванными отверстиями, предназначенное для распыления каких-либо жидкостей (реже порошка). Под распылением при этом понимается распад струй жидкости на мелкие капли.
Сферы применения форсунок весьма обширны. В авиастроении, ракетостроении и автомобилестроении они используются для распыления топлива с целью повышения эффективности его сгорания; в производстве – для нанесения красок и клеев, смазки подшипников, охлаждения инструментов при операциях механической обработки, мойки различных поверхностей; в добывающей промышленности – для уменьшения количества пыли, промывки горных пород; в сельском хозяйстве – для полива и орошения, а также для разбрызгивания ядохимикатов и жидких удобрений; в абсорберах форсунки осуществляют распыление известняковой суспензии для контроля выброса вредных газов (особенно диоксида серы); в полых скрубберах вода распыляется для удаления твёрдых частиц из запылённого газа; в градирнях форсунки являются основным конструктивным элементом, определяющим её охлаждающую способность.
Наиболее важными функциональными и эксплуатационными параметрами форсунок являются: расходно-напорные характеристики, дисперсия распыления (распределение капель по размеру), равномерность орошения поверхности, геометрические характеристики (форма, угол раскрытия и радиус факела разбрызгивания), а также ударная сила струи. Наибольшая трудность при моделировании процессов распыления заключается в получении корректного расчётного набора перечисленных параметров, в особенности это относится к распределению частиц жидкости по размеру и к геометрическим параметрам факела распыления.
В настоящее время существует несколько основных подходов к моделированию процессов распыления. Наиболее точный из них основан на прямом моделировании распада струи c использованием модели Volume of Fluid (VOF), когда весь интересующий диапазон капель разрешается с помощью сеточной модели. Однако данный подход предъявляет очень высокие требования к вычислительным ресурсам, из-за чего в большинстве случаев просто не может быть реализован в полном объёме на практике. Другой гораздо более экономичный подход основан на задании начальных скоростей и размеров капель, которые заранее известны, например, определены в ходе эксперимента или с использованием полуэмпирических моделей первичного распада. Траектории капель и их дальнейшее взаимодействие со сплошной средой (в том числе вторичный распад) рассчитываются с использованием Лагранжевой модели Discrete Phase Model (DPM). Широко применяется гибридный подход, в основе которого лежит модель VOF-to-DPM [1]. В ней первичный распад струи осуществляется путём прямого моделирования в Эйлеровой постановке, а дальнейшее движение жидких масс, размеры которых уже не могут быть разрешены с помощью сеточной модели, рассчитывается в Лагранжевой постановке путём конвертации этих масс в дискретные DPM-капли (рисунок 1).
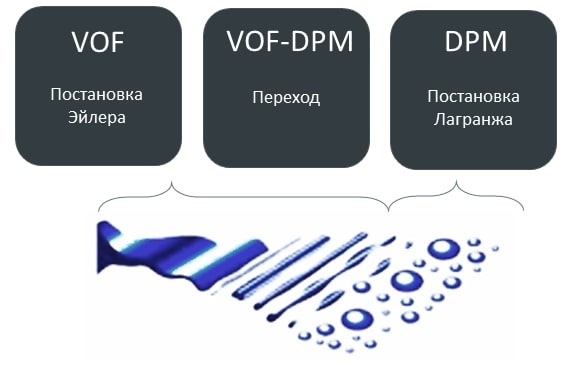
Рисунок 1. Принцип работы модели VOF-to-DPM
Специалисты АО «ЦИФРА» продемонстрировали возможность применения данного гибридного подхода для моделирования тарельчатой форсунки в ПО Ansys Fluent.
Расчётная модель форсунки
На рисунке 2 представлена геометрическая модель тарельчатой форсунки с соплом ударного принципа действия. Форсунки с ударными соплами зачастую используются в конструкциях градирен, поскольку являются наименее энергоёмкими и при этом обладают большим радиусом разбрызгивания. Габариты факелов разбрызгивания и размеры капель в факелах ударных сопел зависят от формы и конструкции отражателя, а также напора воды. Согласно экспериментальным данным [2] радиус факела , измеренный на расстоянии 0,8÷1 м от выхода из сопла при направлении факела вниз, составляет для моделируемой форсунки при объёмном расходе воды 16,2 мᶾ/ч около 1,8 м.
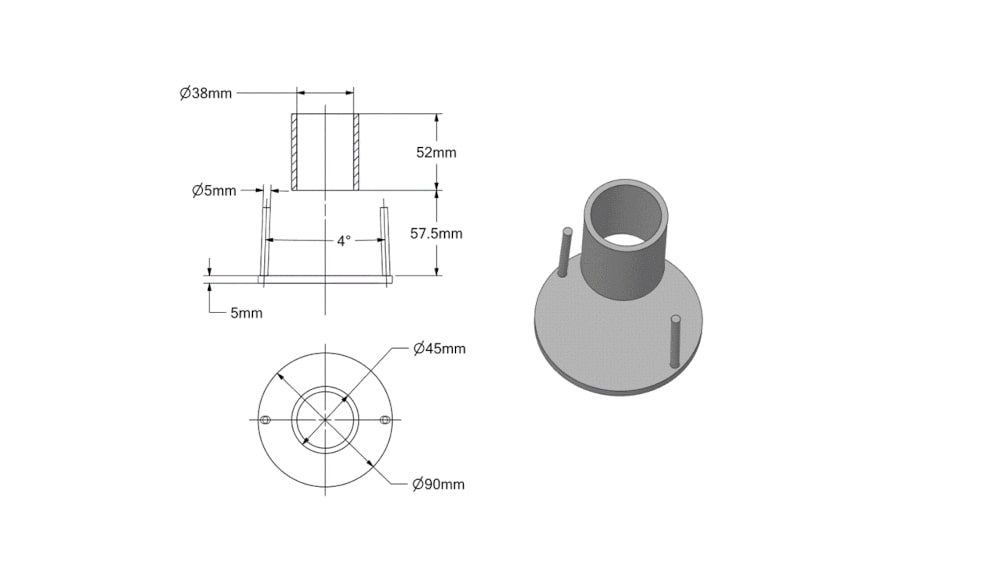
Рисунок 2. Геометрия моделируемой тарельчатой форсунки
Внешний вид расчётной области представлен на рисунке 3. Внутри расчётного домена построено вспомогательное тело (body of influence), используемое для локального измельчения расчётной сетки в области первичного распада струй.
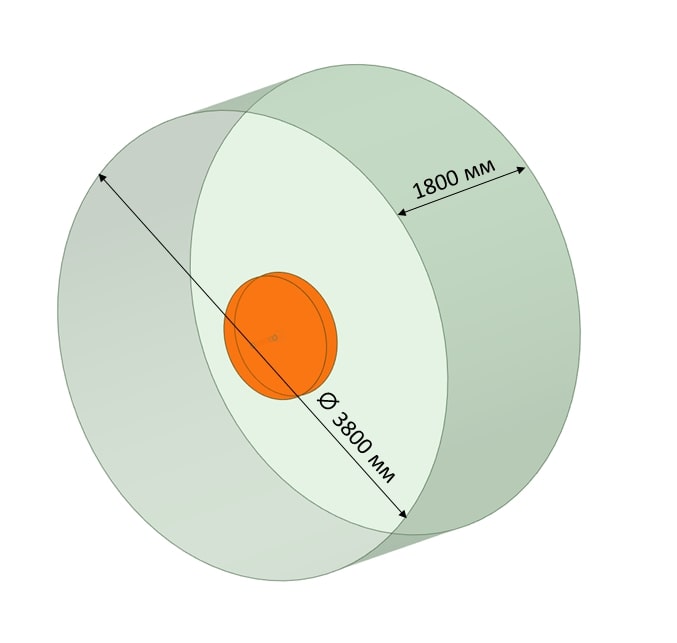
Рисунок 3. Габариты расчётной области
В начале расчёта сеточная модель состоит приблизительно из 2,2 млн ячеек. В ходе нестационарного расчёта с периодичностью один раз в пять временных шагов применена опция динамической адаптации сетки. Данная опция позволяет дополнительно измельчать сетку на границе раздела сред воздух-вода, а также загрублять сетку в тех областях течения, где осуществлена конвертация жидких структур в DPM-капли. Внешний вид фрагмента сеточной модели в осевом сечении форсунки с учётом динамической адаптации спустя 0,05 секунд с момента начала расчёта представлен на рисунке 4. Число элементов в сеточной модели в ходе динамической адаптации находится в пределах 6 млн с учётом заданных в процессе решения ограничений.
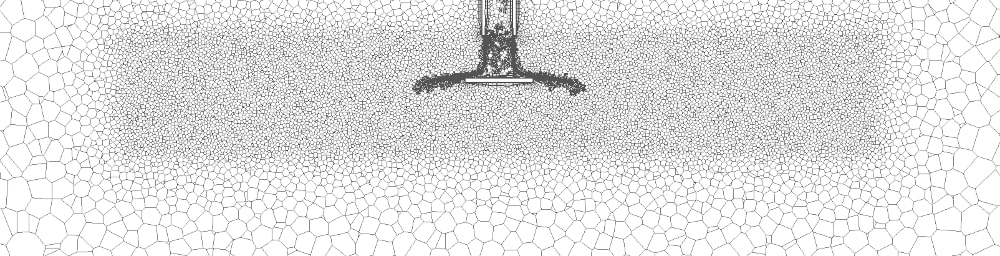
Рисунок 4. Фрагмент сеточной модели в осевом сечении форсунки спустя 0,05 секунд с момента начала расчёта
Результаты моделирования
На рисунке 5 показаны результаты моделирования распылительной форсунки с ударным соплом с использованием модели VOF-to-DPM на момент расчётного времени 0,3 секунды. Попадая на тарельчатый отражатель, поток воды разбивается на отдельные тонкие струи. Далее при соответствии изолированных масс жидкости ряду критериев, предварительно настроенных в соответствующей вкладке для модели VOF-to-DPM, происходит конвертация этих жидких структур в дискретные капли. Распределение дискретных капель по размерам также приведено на рисунке 5, при этом DPM-капли для большей наглядности отрисованы в виде точек.
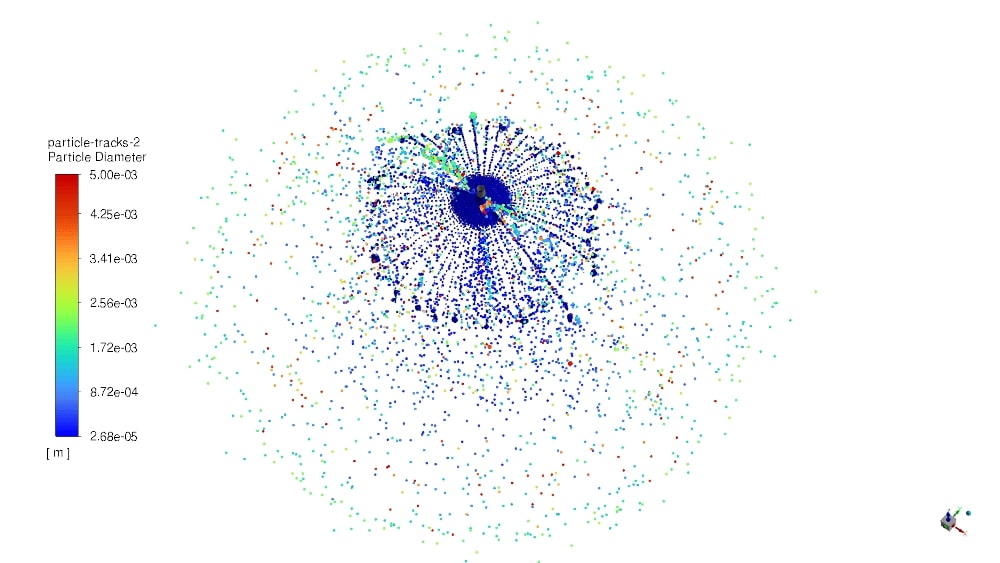
Рисунок 5. Результаты моделирования распылительной форсунки с ударным соплом с использованием модели VOF-to-DPM
На рисунке 6 приведено распределение объёмной доли воды в Эйлеровой постановке. Видно, что при увеличении размеров сеточных ячеек представление жидких структур становится слишком грубым. Это свидетельствует о том, что для получения точных результатов в рамках модели VOF-to-DPM следует применять более подробные сетки, однако, данное решение носит скорее демонстрационный характер, и при необходимости может быть реализовано на более подробных сетках с помощью высокопроизводительной вычислительной техники.

Рисунок 6. Распределение объёмной доли Эйлеровой жидкой фазы
Расчётный процесс распыления воды рассматриваемой форсункой с использованием модели VOF-to-DPM в течение 0,3 секунд расчётного времени приведён на анимации 1. По итогам расчёта на отметке 0,85 м ниже выхода из сопла осуществлён замер радиуса факела , который составляет около 1,5 м, что с учётом низкого уровня дискретизации расчётной сетки неплохо согласуется с экспериментальными данными.

Анимация 1. Расчётный процесс распыления воды форсункой с ударным соплом
Заключение
По итогам моделирования тарельчатой форсунки с использованием модели VOF-to-DPM получены объёмные цветовые карты Эйлеровой и Лагранжевой фаз. Полное давление при подходе жидкости к соплу форсунки при указанном её расходе составляет около 8 кПа. Расчётный радиус факела на расстоянии 0,85 м от сопла приблизительно равен 1,5 м, что неплохо согласуется с экспериментальными данными. Максимальный радиус факела в нижнем сечении построенной расчётной области, по оценкам специалистов АО «ЦИФРА», при продолжении расчётного процесса составит около 1,8-1,9 м, что сопоставимо с радиусом расчётного домена. Использованная в расчёте сеточная модель позволяет лишь грубо смоделировать процесс распыления жидкости. Для более точного описания требуется использовать более подробную расчётную сетку и прибегать к применению высокопроизводительной вычислительной техники.
Список использованных источников
- Ansys Fluent, Release 2021 R2, Help System, Fluent help, user manual, 22.3.13 Using the VOF-to-DPM model transition for dispersion of liquid in gas, ANSYS, Inc.
- Пономаренко В.С., Арефьев Ю.И. Градирни промышленных и энергетических предприятий: Справочное пособие. Москва: Энергоатомиздат, 1998. 376 с.

.png)





