Специалистами АО «ЦИФРА» продемонстрирована возможность применения численного моделирования для определения сопротивления объектов, обтекаемых сверхзвуковым/гиперзвуковым потоком, на примере решения тестовой задачи в программном пакете Ansys Fluent с последующей верификацией полученных результатов.
Определение сопротивления тел на различных режимах полёта – одна из важнейших задач практической аэродинамики. Полученные данные необходимы как для проектирования новых образцов авиационной и ракетно-космической техники, так и для оценки эффективности и оптимизации уже имеющихся. Сопротивление тела зависит от множества факторов: от его формы и размеров; скорости и угла атаки; шероховатости его поверхности; свойств среды, в которых оно движется и т.д. Поэтому, несмотря на то что накопление экспериментальных данных продолжается уже более столетия, задача определения сопротивления тел все ещё остаётся актуальной. Альтернативой натурным экспериментам в этой области может стать численное моделирование.
Физические особенности сверхзвукового обтекания твёрдых тел
На малых (дозвуковых) скоростях сопротивление тела обусловлено действием на него сил давления и трения со стороны потока. Для хорошо обтекаемых тел (например, тонкая пластина, расположенная под малым углом по направлению к потоку) сопротивление вызвано преимущественно действием сил трения со стороны набегающего потока, в то время как для плохообтекаемых тел, с которых поток срывается, образуя вихревую зону разрежения (например, цилиндр или сфера), больший вклад в результирующее сопротивление вносят силы давления.
На сверхзвуковых скоростях вклад сил трения и давления в результирующее сопротивление становится не столь существенным в сравнении с вкладом волновой составляющей, связанной с образованием скачка уплотнения. Скачком уплотнения называют область малой толщины (порядка длины свободного пробега молекул), характерную для сверхзвукового обтекания тел, в которой резко возрастают плотность, температура и давление, ввиду преобразования части кинетической энергии сверхзвукового потока в энергию давления и тепловую энергию.
Постановка задачи
В таблице 1 приведены основные расчётные параметры. Тестовая задача поставлена таким образом, чтобы полученные результаты можно было сверить с экспериментальными данными. В работе [1] исследовано обтекание сферы диаметром 9,525 мм при различных числах Маха и показано, что в диапазоне чисел Маха 4÷10 коэффициент сопротивления сферы практически не меняется и составляет около 0,92.
Таблица 1 – Исходные данные
| Число Маха | 5 |
| Скорость звука в области эксперимента | 335 м/с |
| Скорость потока воздуха в расчёте | 1675 м/с |
| Атмосферное давление в области эксперимента | 84559 Па |
| Плотность воздуха в области эксперимента | 1,0581 кг/м3 |
| Диаметр сферы | 9,525 мм (3/8 дюйма) |
| Характерная площадь (площадь миделевого сечения) | 71,256 мм2 |
Расчётная область представляет собой цилиндр с диаметром, равным семи диаметрам сферы (рисунок 1). Поскольку задача является симметричной, в целях экономии вычислительных ресурсов рассмотрена только половина сферы.
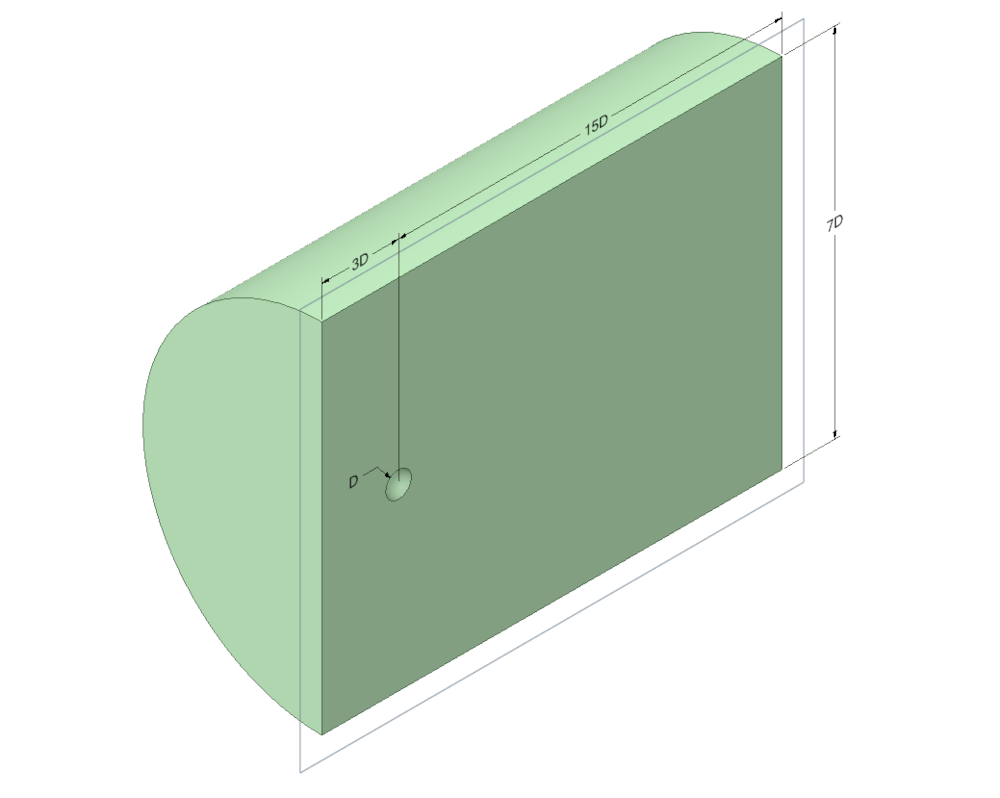 Рисунок 1 – Геометрия расчётной области
Рисунок 1 – Геометрия расчётной области
Используемые граничные условия показаны на рисунке 2.
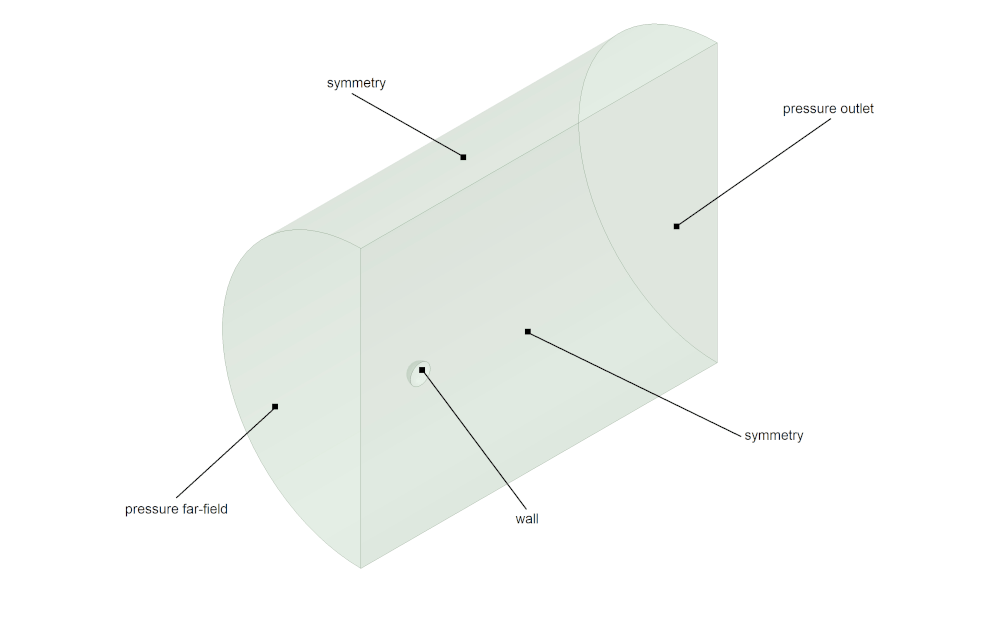 Рисунок 2 – Используемые граничные условия
Рисунок 2 – Используемые граничные условия
Для решения задачи построено несколько сеточных моделей с различным количеством элементов, представленных в виде многогранников произвольной формы. Параметры сеточных моделей приведены в таблице 2.
| № | Число ячеек | Расчётный коэффициент сопротивления |
| 1 | 81 000 | 0.9326 |
| 2 | 133 000 | 0.9305 |
| 3 | 222 000 | 0.9328 |
| 4 | 454 000 | 0.9338 |
| 5 | 959 000 | 0.9336 |
| 6 | 1 755 000 | 0.9325 |
| 7 | 3 299 000 | 0.9342 |
Таблица 2 – Используемые для оценки сеточной сходимости сеточные модели
Критерием для оценки сеточной сходимости выбран коэффициент сопротивления сферы: при изменении данного параметра в пределах 1–2 % относительно наиболее подробной сеточной модели можно полагать, что сеточная сходимость достигнута. График зависимости коэффициента сопротивления от количества ячеек сетки приведён на рисунке 3. Коэффициент сопротивления определяется как отношение силы сопротивления к скоростному напору и характерной площади обтекаемого тела:
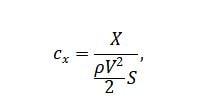
где 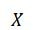 – сила сопротивления (составляющая аэродинамической силы, направленная против движения тела);
– сила сопротивления (составляющая аэродинамической силы, направленная против движения тела);
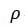 – плотность воздуха;
– плотность воздуха;
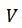 – скорость воздуха;
– скорость воздуха;
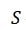 – характерная площадь (в данной задаче – площадь миделевого сечения).
– характерная площадь (в данной задаче – площадь миделевого сечения).
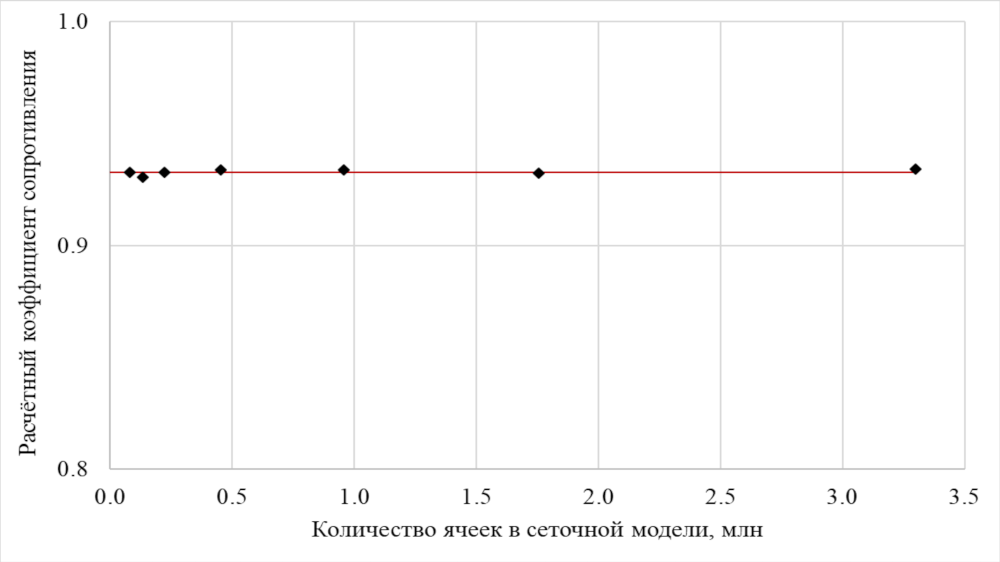 Рисунок 3 – График зависимости расчётного коэффициента сопротивления от количества ячеек в сеточной модели
Рисунок 3 – График зависимости расчётного коэффициента сопротивления от количества ячеек в сеточной модели
Как видно из таблицы и рисунка, результаты на грубых и подробных сетках различаются несущественно. Так, среднеквадратичное отклонение для всей рассматриваемой выборки составляет около 0,11 %, в связи с чем можно заключить, что для рассмотренных сеточных моделей решение является сеточно-независимым.
Внешний вид сеточной модели №4, выбранной для дальнейшего исследования, показан на рисунке 4.
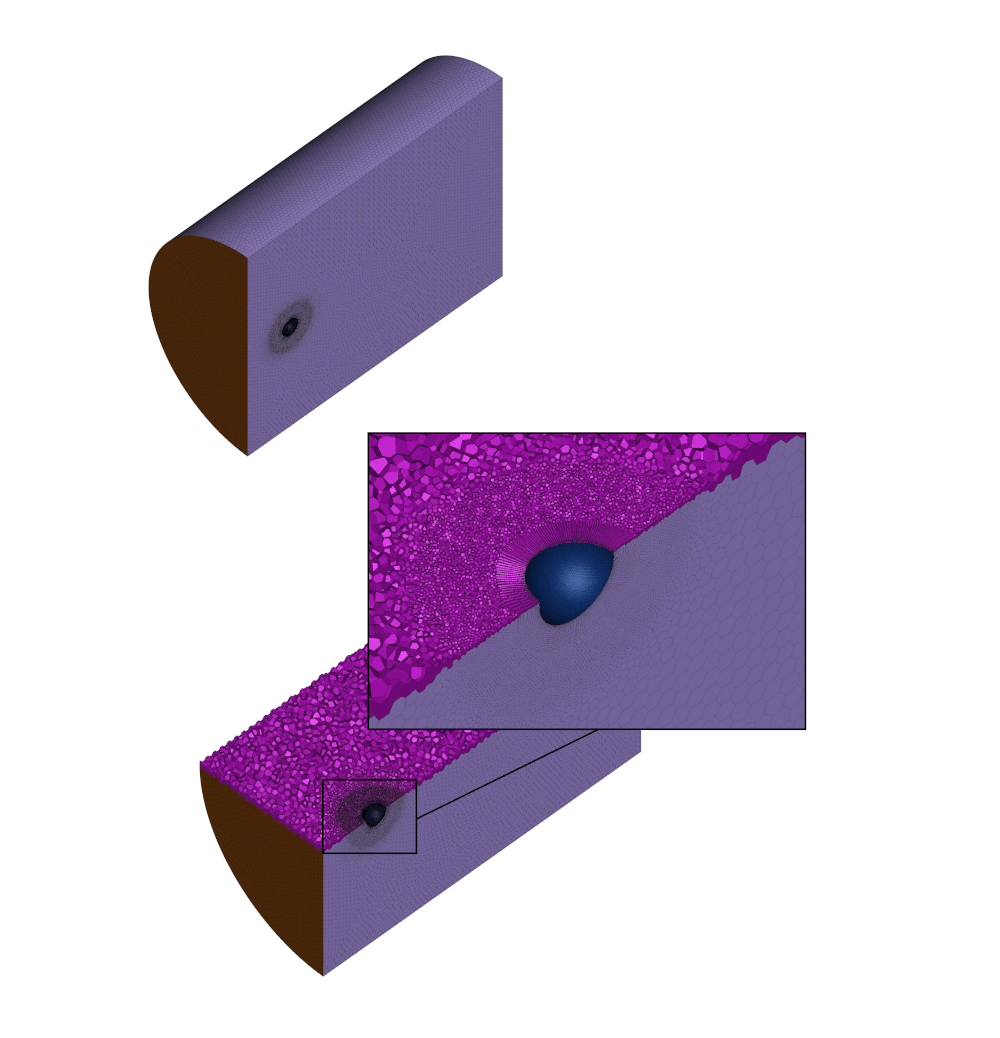 Рисунок 4 – Расчётная сеточная модель
Рисунок 4 – Расчётная сеточная модель
С целью достижения более качественного разрешения области скачка уплотнения в ходе расчёта с регулярностью раз в 100 расчётных итераций применена опция автоматической адаптации сетки. Сошедшееся решение достигнуто за 1000 итераций. Исходная и конечная сеточные модели показаны на рисунке 5. Как будет продемонстрировано далее, сгущение сетки реализовано в областях наибольших градиентов параметров потока.
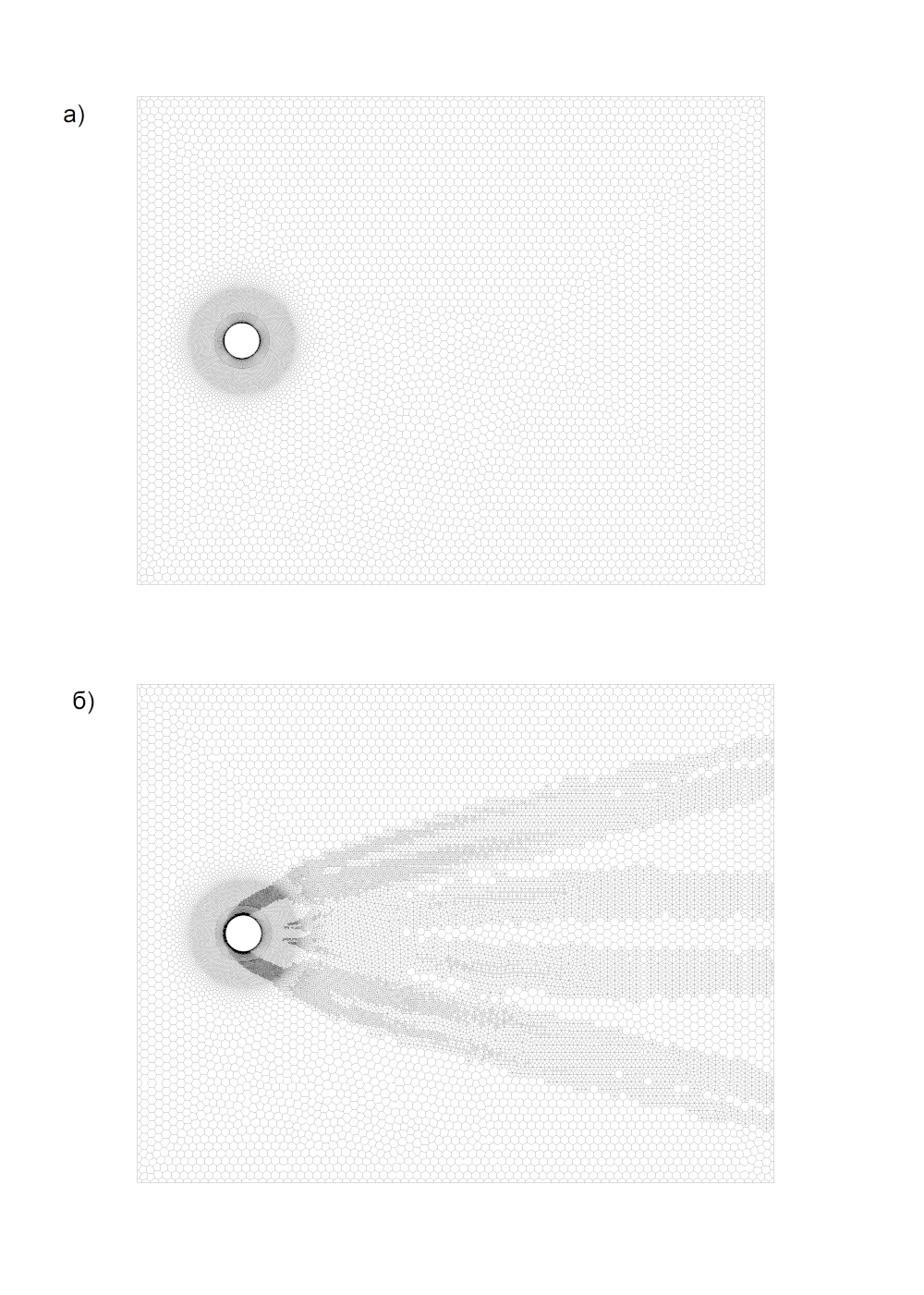 а) – исходная сетка; б) – итоговая сетка.
а) – исходная сетка; б) – итоговая сетка.
Рисунок 5 – Результаты автоматической адаптации сетки
Результаты моделирования
На рисунках 6–9 показаны распределения чисел Маха, давления, плотности и температуры в плоскости симметрии расчётной модели (миделевое сечение сферы).
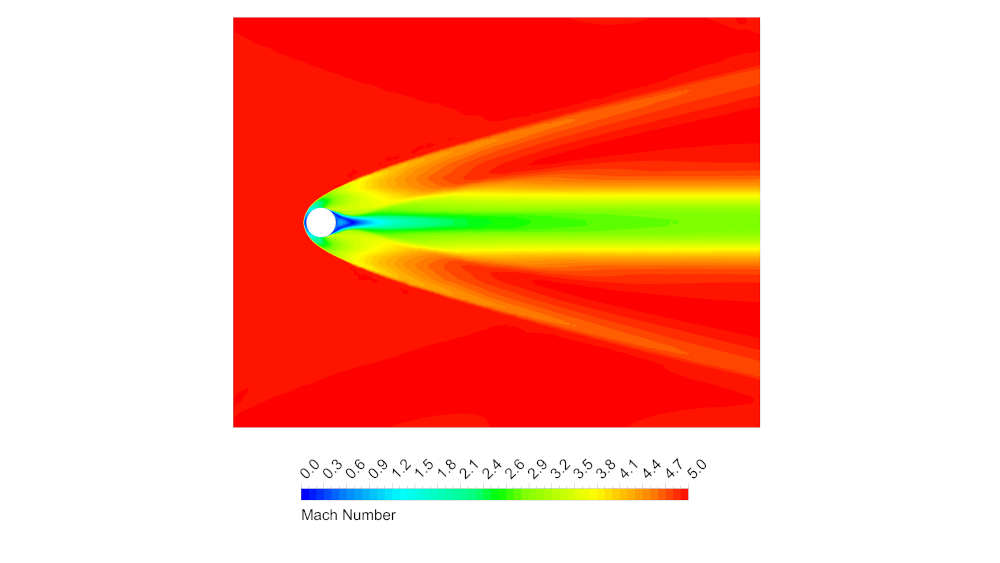 Рисунок 6 – Распределение чисел Маха в плоскости симметрии сферы
Рисунок 6 – Распределение чисел Маха в плоскости симметрии сферы
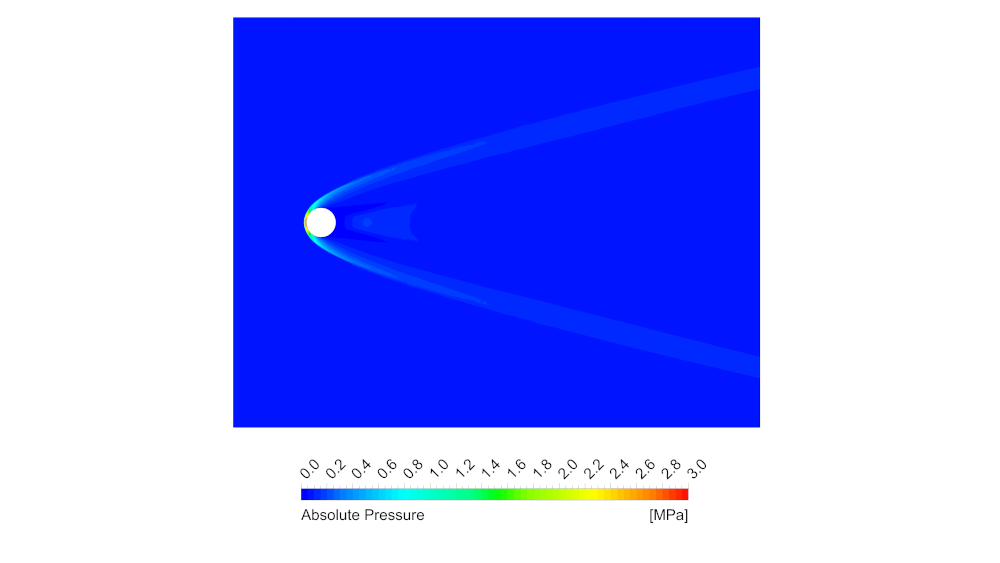 Рисунок 7 – Распределение абсолютного давления в плоскости симметрии сферы
Рисунок 7 – Распределение абсолютного давления в плоскости симметрии сферы
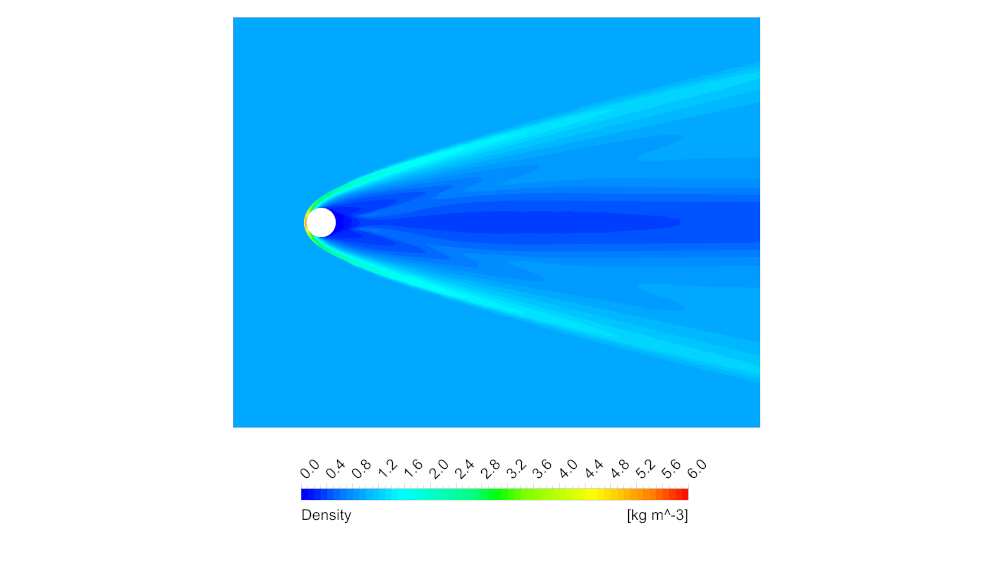 Рисунок 8 – Распределение плотности в плоскости симметрии сферы
Рисунок 8 – Распределение плотности в плоскости симметрии сферы
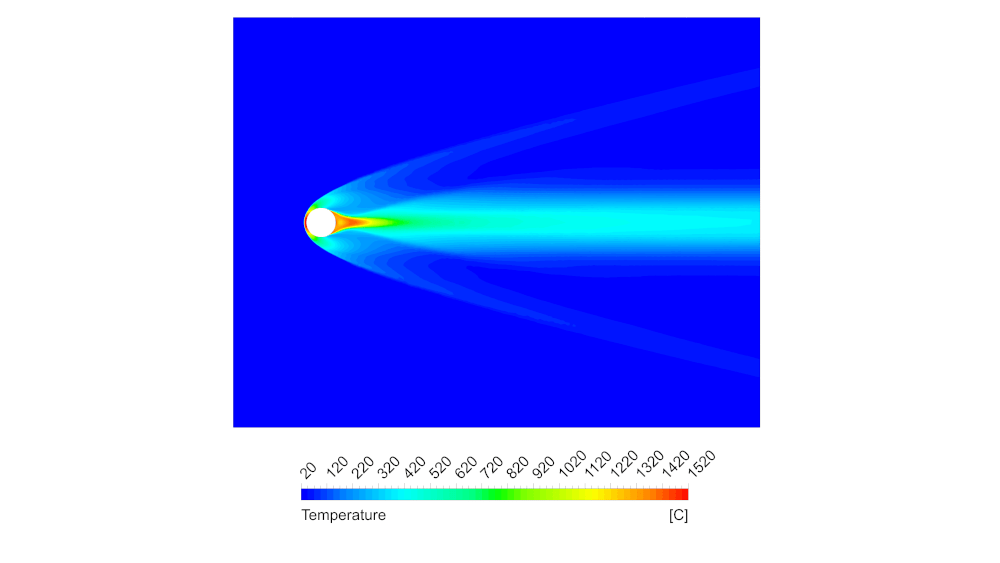 Рисунок 9 – Распределение температуры в плоскости симметрии сферы
Рисунок 9 – Распределение температуры в плоскости симметрии сферы
Полученные расчётные поля визуально соответствуют результатам эксперимента для числа Маха 4, приведённым в работе [2] (рисунок 10). Из этого можно сделать вывод о том, что расчётные результаты являются качественно верными.
 Рисунок 10 – Спектр обтекания сферы при числе Маха 4
Рисунок 10 – Спектр обтекания сферы при числе Маха 4
О количественной достоверности результатов можно судить по величине полученного коэффициента сопротивления, составляющей примерно 0,9343, тогда как экспериментально полученное значение равно 0,92. Расхождение составляет приблизительно 1,09%, что с учётом экспериментальных и расчётных погрешностей является вполне допустимым.
Можно заключить, что численное моделирование представляет собой альтернативу натурному моделированию, обеспечивая достаточную точность при значительно меньших временных и финансовых затратах. Опыт, полученный специалистами АО «ЦИФРА» при решении данной тестовой задачи, может быть экстраполирован на моделирование обтекания более сложных тел.
Используемые источники
1.Hodges, A. J., «The Drag Coefficient of Very High Velocity Spheres», J. Aero. Sci., Vol. 24, No. 10, October 1957, pp 755-758
2.С.И. Герасимов, В.А. Кикеев, К.В. Тотышев, А.П.Фомкин, Б.А. Яненко. Визуализация сверхзвукового движения сферы в воздухе и в воде

.png)





