Используя методы численного моделирования, специалисты АО «ЦИФРА» провели тепловой расчёт пофазно-экранированного токопровода с учётом влияния инсоляции (воздействие прямых солнечных лучей на поверхность).

Сфера использования токопроводов очень велика: они могут применяться на тепловых электростанциях, крупных блочных электростанциях, атомных электростанциях, гидроэлектростанциях, гидроаккумулирующих электростанциях и т. д. Токопровод предназначен для передачи и распределения электрической энергии, как правило, между блоками одной электроустановки. Пример токопроводов представлен на рисунке 1.

Рисунок 1 – Пример токопроводов АЭС

Во время эксплуатации токопровода возникает риск его перегрева, так как вся энергия потерь при прохождении тока через токопровод переходит в тепло. При разработке и проектировании подобного рода систем важно оценить максимальную температуру, достигаемую на поверхности оборудования во время его работы, в том числе при воздействии инсоляции.

Процесс проведения теплового расчёта условно можно разделить на несколько этапов, таких как разработка геометрической трёхмерной CAD модели, построение сеточной модели, настройка численной модели и граничных условий (ГУ), непосредственно проведение расчёта и анализ расчётных результатов.

Геометрическая модель

Разработанная CAD-модель токопровода включает в себя кожухи, шины, шинные компенсаторы, проходной изолятор и систему принудительного охлаждения (рисунок 2).

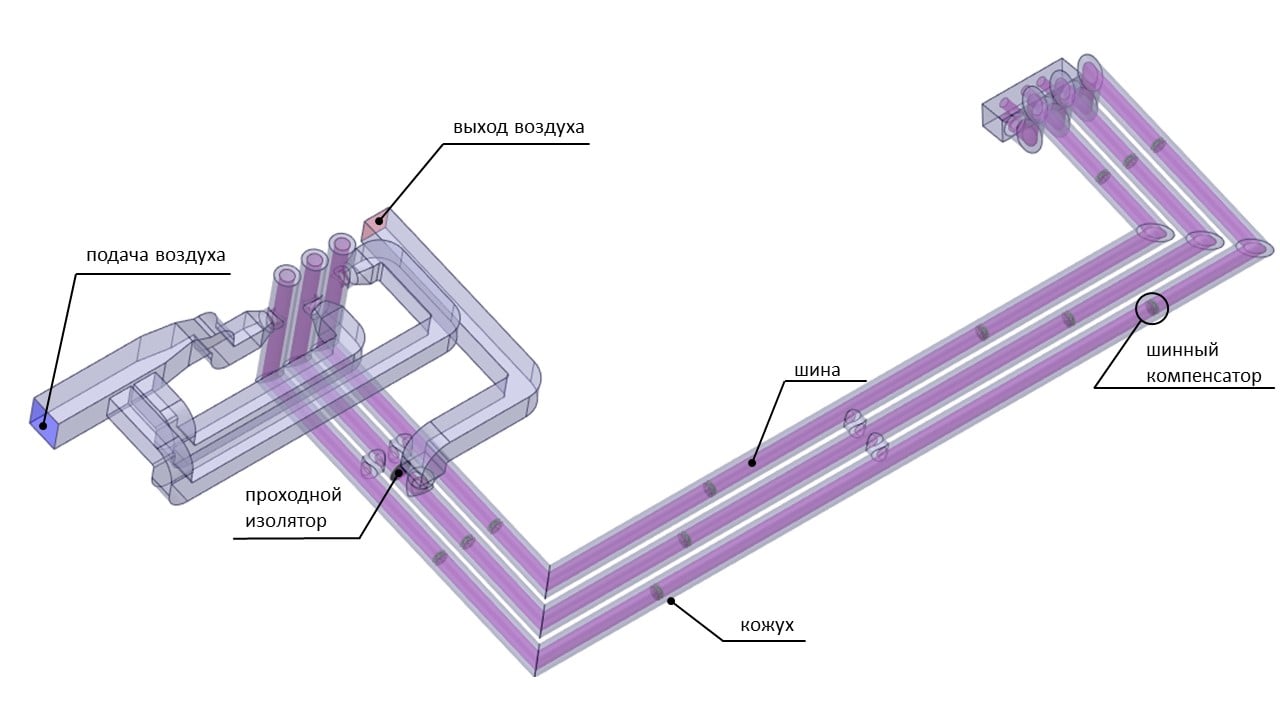
Рисунок 2 – Геометрическая трёхмерная CAD-модель токопровода

Кожухи защищают токоведущие шины от влияния окружающей среды, поэтому основное воздействие инсоляции приходится именно на них. Шинные компенсаторы позволяют перемешивать внутренний и внешний поток и компенсировать деформации, обусловленные температурными перепадами.

Система принудительного охлаждения представляет собой в данном случае три воздуховода, предназначенные для подачи воздуха в систему, а также воздуховод для отвода нагретого воздуха из системы. 

Сеточная модель

Для подготовленной геометрической модели в программном модуле Fluent Meshing разработана сеточная модель конечных объёмов. Количество элементов расчётной сетки составляет 1,7 млн. ячеек.  Фрагмент сеточной модели представлен на рисунке 3. 

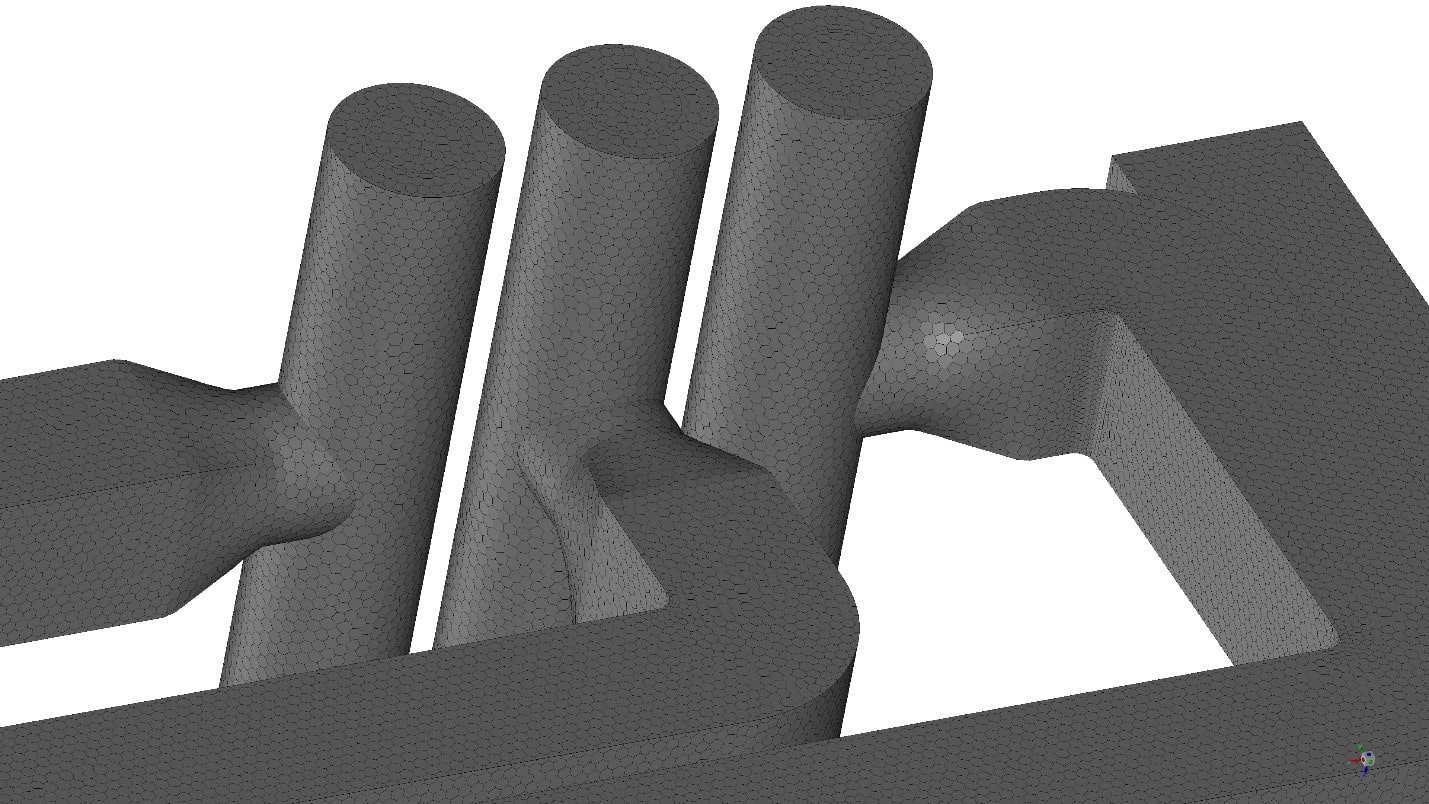
Рисунок 3 – Фрагмент сеточной модели вблизи воздуховодов для подачи воздуха в систему

Для уточнённого моделирования течений вблизи твёрдых стенок, вдоль них построено три призматических слоя ячеек (рисунок 4).

Рисунок 4 – Призматические слои в сечении сеточной модели

Постановка задачи

Массовый расход воздуха, подаваемый в систему, составляет 12 кг/с, температура воздуха 30 °С. Для расчёта турбулентного конвективного течения потока воздуха, возникающего в процессе вынужденной конвекции, применяется метод интегрирования уравнений Навье—Стокса, осреднённых по Рейнольдсу (RANS модель), предполагающих нахождение решения в виде полей параметров течения, осреднённых по времени. Для замыкания системы уравнений Навье—Стокса, осреднённых по Рейнольдсу, выбрана модель турбулентности  k—ω Shear Stress Transport (k—ω SST). Данная модель предполагает изотропность турбулентности и моделирование потока в пристеночном слое, не зависящее от характерного размера в первом пристеночном слое ячеек. Давление на выходе из системы принимается равным атмосферному.

На всех твёрдых стенках модели токопровода используется ГУ гидродинамически гладкой стенки, что соответствует равенству нулю вектора скорости и градиентов всех параметров течения.

В ходе моделирования используется модель излучения Surface to Surface (S2S), которая предназначена для расчёта теплопередачи от поверхности к поверхности через оптически тонкую среду. Для не запылённого воздуха значение оптической толщины во много раз меньше 1, что даёт основание считать рассматриваемую среду оптически прозрачной.

На внешних стенках кожухов и воздуховодов задаётся тепловое ГУ третьего рода, предполагающее задание температуры внешней текучей среды и закона теплообмена между поверхностью твёрдого тела и окружающей средой. Это отражает в первом приближении сложный лучистый и конвективный теплообмен, в котором доля лучистого потока теплоты является преобладающей. Температура внешней среды задаётся равной 30 °С. Значение коэффициента внешней теплоотдачи (для неподвижного воздуха) выбрано равным 5 Вт/м^2∙К из консервативных соображений. 

На стенках шин, шинных компенсаторов, проходного изолятора, а также внутренних стенках кожухов и воздуховодов в модели задаётся ГУ сопряжённой теплопередачи. Помимо прочего для шин и кожухов задаются значения удельных потерь энергии.

Значения коэффициентов излучения для всех внутренних стенок модели составляет 0,9, для внешних — 0,11.

Для оценки влияния инсоляции на поля температур произведено последовательно два расчёта: с учётом инсоляции и без учёта инсоляции. Остальные ГУ в обоих расчётах при этом не изменялись.

Решение задач осуществлялось в стационарной постановке, для выхода на режим установления потребовалось около 1000 итераций для каждого расчётного случая.

В расчёте с учётом инсоляции в качестве расчётного направления солнечного потока выбрано направление перпендикулярное к горизонтальной плоскости, в которой расположен токопровод. В расчёте значение потока солнечного излучения принималось равным 600 Вт/м^2. Солнечный поток воздействует на все поверхности токопровода, не находящиеся в производственном помещении (рисунок 5). 

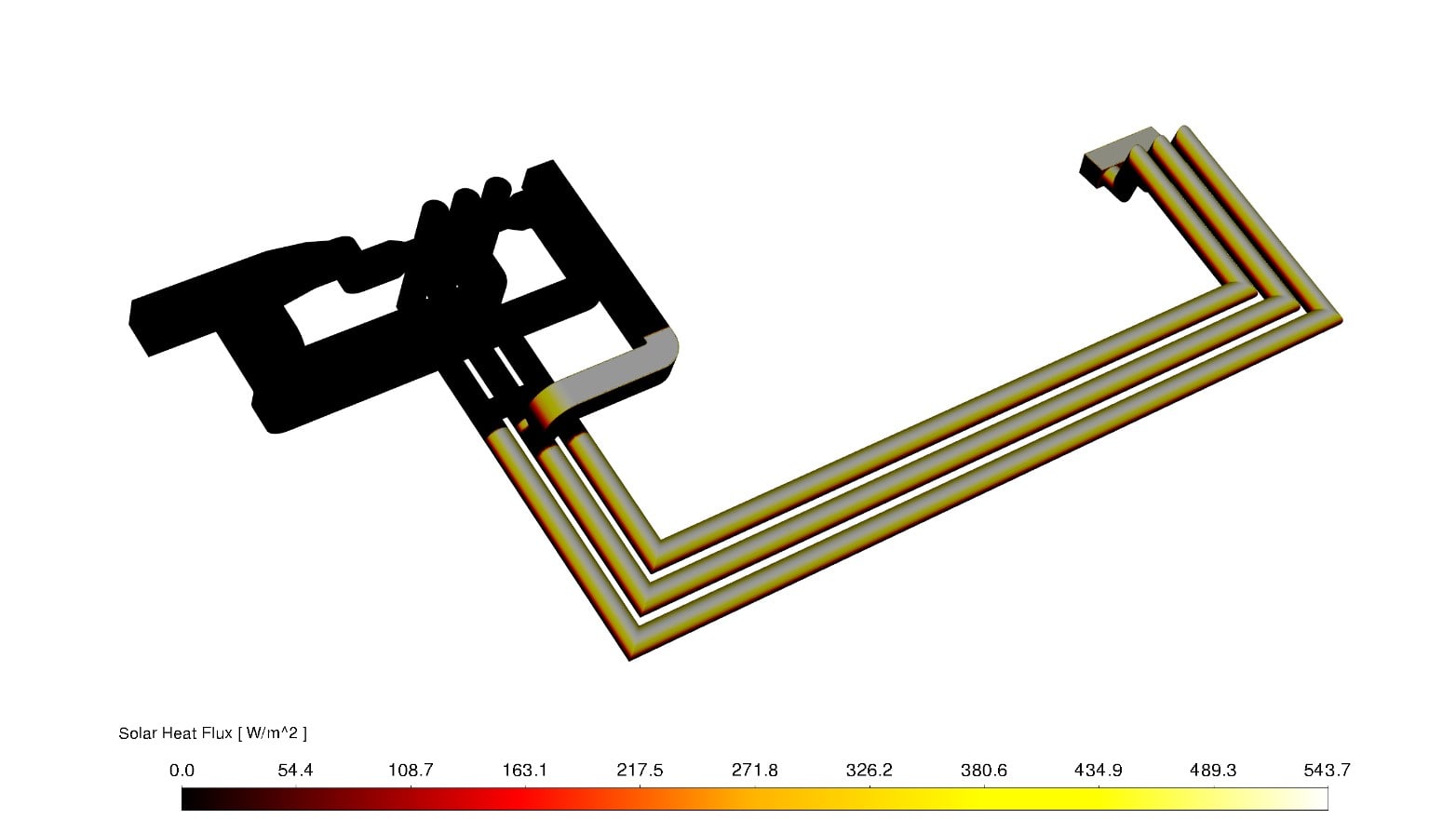
Рисунок 5 – Распределение потока солнечного излучения по поверхности токопровода

Результаты расчётов

В результате проведения расчёта с учётом инсоляции получено распределение температуры по поверхностям кожухов и шин. Наибольшее влияние солнечного потока приходится на верхнюю поверхность кожухов, где отчётливо прослеживаются области достижения максимальной температуры, равной 73 °С. Минимальные температуры наблюдаются на поверхности воздуховодов, находящихся в производственном помещении.

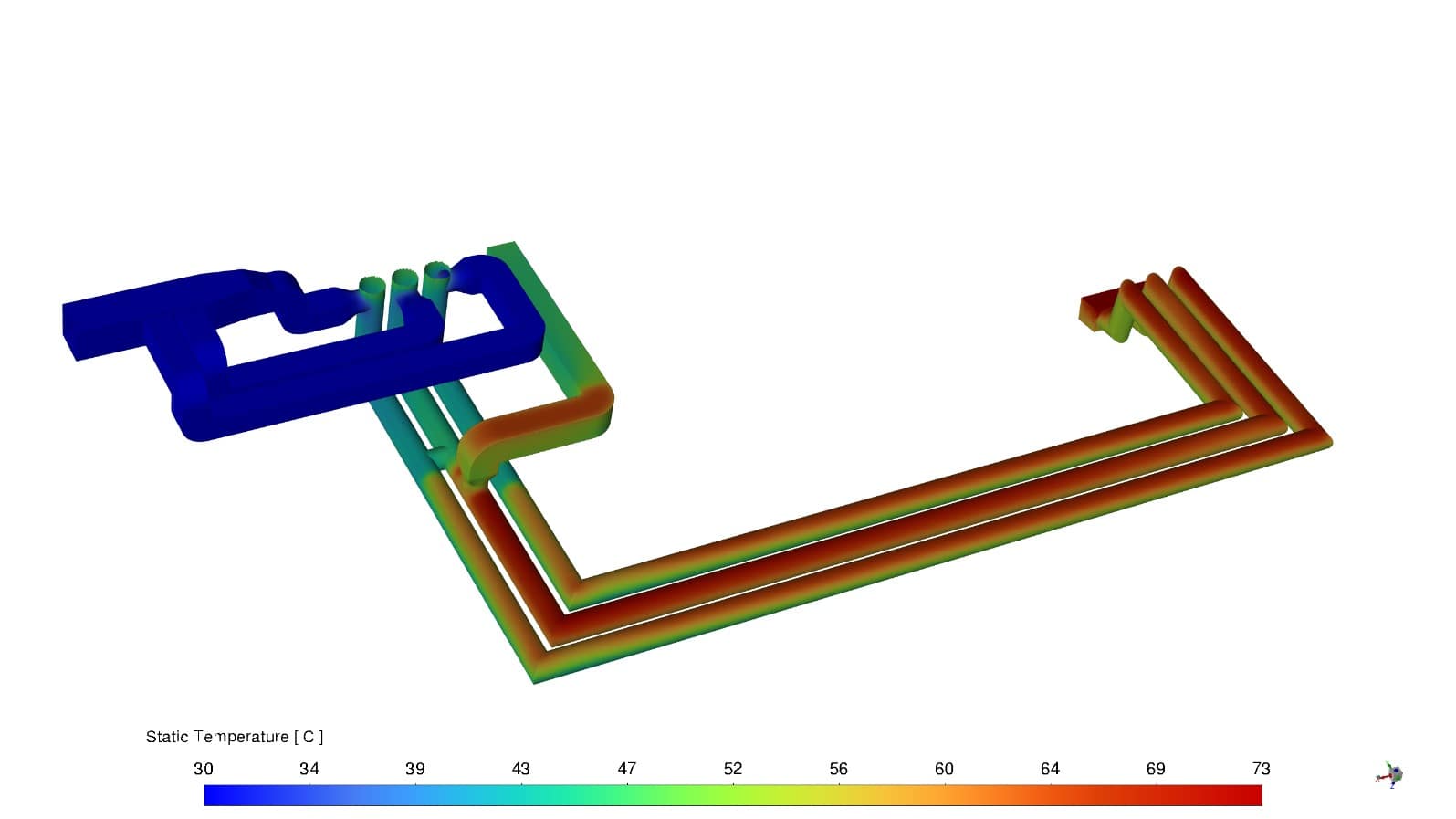
Рисунок 6 – Распределение температуры по поверхности кожухов с учётом инсоляции

На рисунке 7 представлено соответствующее распределение температуры по поверхности шин. Максимальная температура составляет 95 °С.

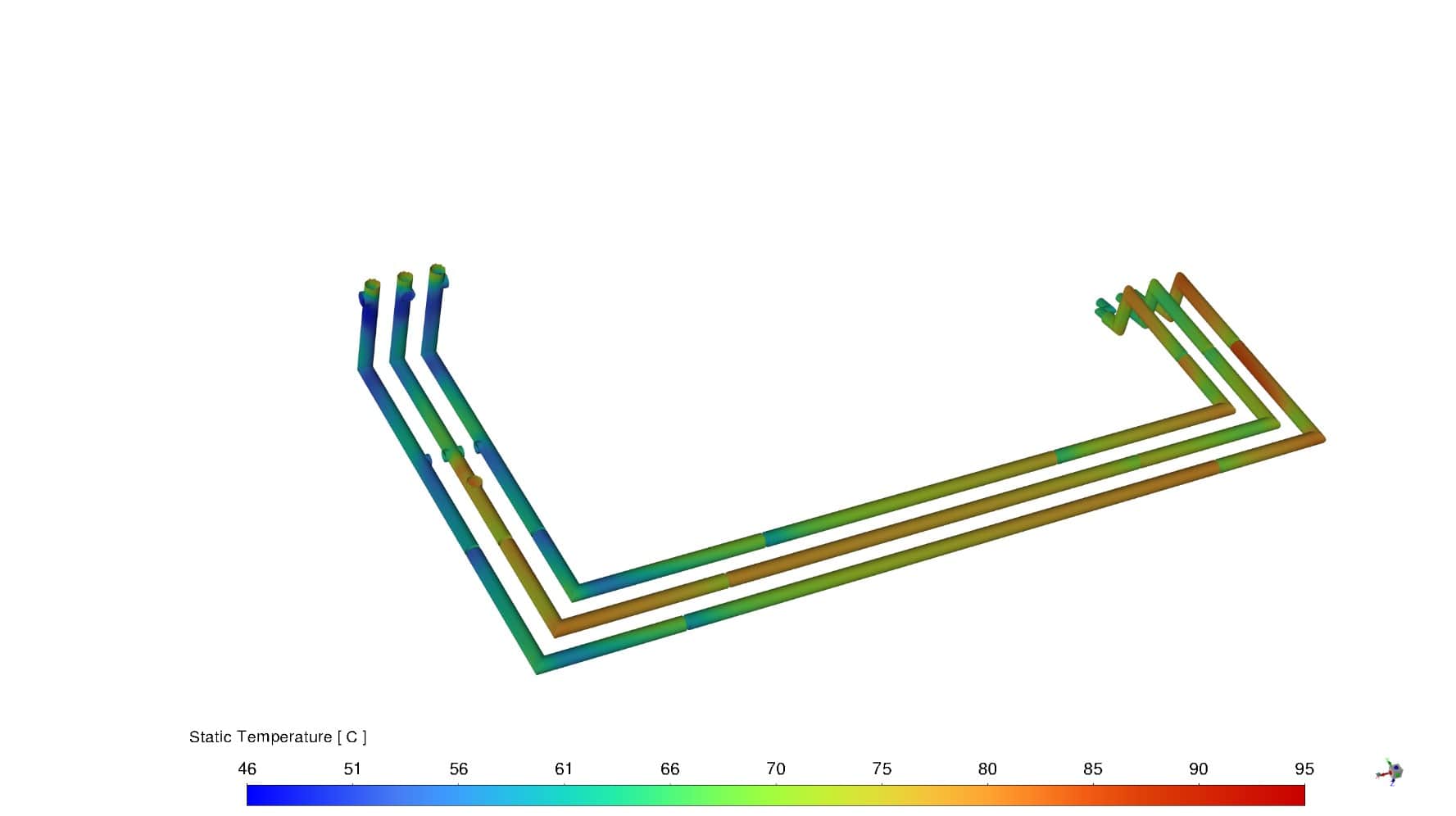
Рисунок 7 – Распределение температуры по поверхности шин с учётом инсоляции

На рисунке 8 показано распределение температуры по поверхности кожухов без учёта инсоляции. Максимальная температура составляет 56 °С. Таким образом, учёт в расчёте инсоляции приводит к увеличению максимальной температуры на поверхности кожухов на 17 °С.

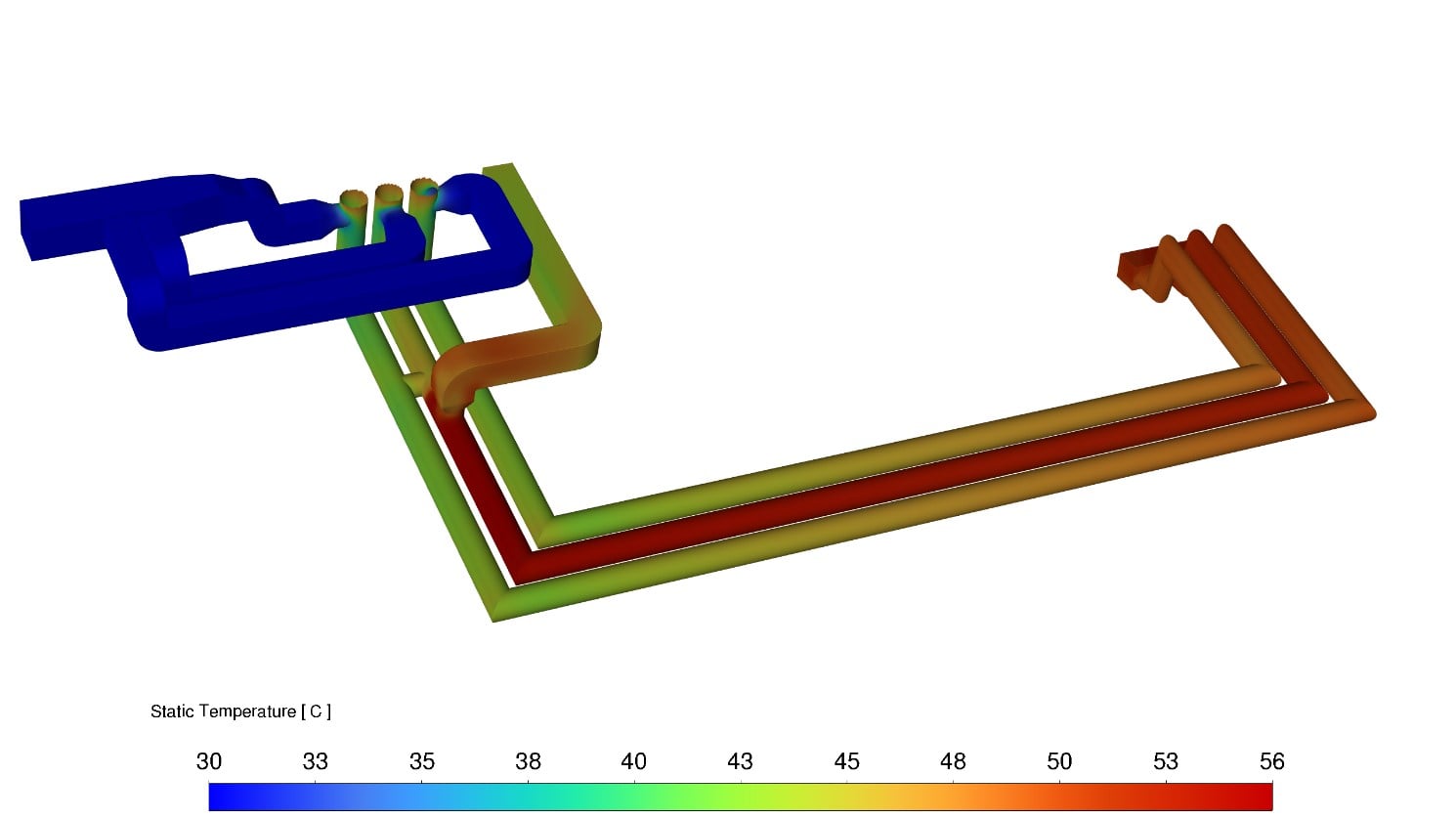
Рисунок 8 – Распределение температуры по поверхности кожуха без учёта инсоляции

Учёт инсоляции приводит и к увеличению температуры на поверхности шин. Максимальная температура на поверхности шин в расчёте без учёта инсоляции составляет 83 °С, что на 12 °С меньше, чем в расчёте с учётом инсоляции (рисунок 9).

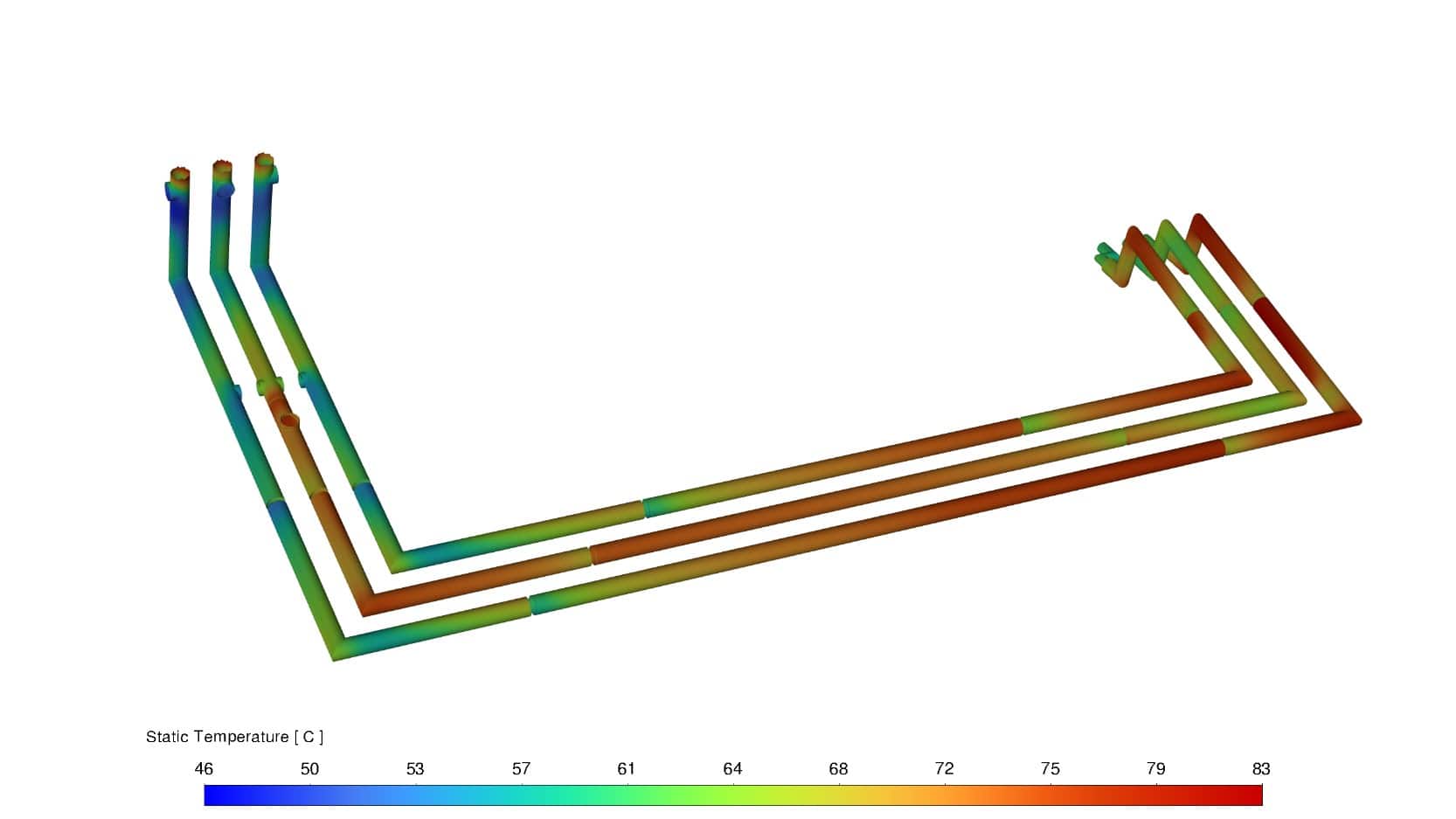
Рисунок 9 – Распределение температуры по поверхности шины без учёта инсоляции

Заключение

Анализ результатов тепловых расчётов показывает, что инсоляция оказывает существенное влияние на распределение температуры по поверхностям конструктивных элементов токопровода, в том числе на максимальное значение температуры, особенно на поверхностях кожухов. Поэтому пренебрегать учётом инсоляции в подобных расчётах не рекомендуется.

Подобное исследование позволяет оценить влияние инсоляции на тепловое состояние объекта ещё на стадии проектирования и подобрать систему охлаждения, способную поддерживать оборудование в работоспособном состоянии, в частности при эксплуатации в экстремально жарких условиях.