Идеальная оптическая система существенно отличается от реальной, так как в реальности на оптическую систему воздействуют тепловые и механические нагрузки, оптические элементы взаимодействуют с конструктивным окружением, вследствие чего приходится сталкиваться с множеством проблем и факторов, которые требуется учитывать и корректировать, чтобы результат проектирования оптического элемента оказался качественным. Учесть большое количество факторов, избежать нежелательных поломок и сэкономить ресурсы за счёт уменьшения натурных испытаний возможно с применением инструментов предсказательного моделирования.
Специалистами АО «ЦИФРА» разработана методика определения деформации рабочей поверхности оптического элемента путём математического моделирования. В сотрудничестве с АО «ЛОМО» проведён эксперимент по нагреву линзы, изготовленной из оптического стекла марки К8 и определению деформации её рабочей поверхности. Для отработки методики для данной линзы поставлена задача, моделирующая условия эксперимента и проведено сравнение результатов эксперимента с результатами моделирования.
Объектом исследования является оптический элемент типа «линза» диаметром 160 мм с толщиной 14,68 мм, представленный на рисунке 1.

Рисунок 1 – объект исследования
Методика определения деформации рабочей поверхности
При воздействии любой нагрузки на оптический объект происходит не столько перемещение самого объекта, сколько искривление (деформация) его рабочих поверхностей, что в свою очередь напрямую влияет на качество получаемого изображения.
Методика заключается в определении среднеквадратичного отклонения (далее СКО) от поля деформации рабочей поверхности оптического элемента. Полученное значение используется оптиками для определения потери качества (разрешения) получаемой картинки.
В рамках первого шага необходимо:
- определить угловые перемещения оптического элемента как единого жёсткого целого вокруг осей перпендикулярных оптической оси;
- определить линейное перемещение линзы как единого жёсткого целого вдоль оптической оси.
Определение поля деформации рабочей поверхности оптического элемента осуществляется путём исключения линейных и угловых компонентов перемещений из поля перемещений вдоль оптической оси.
В рамках второго шага необходимо:
- осуществить перенос данных по полям деформаций поверхности оптического элемента в ПО Excel с последующим расчётом СКО. Ниже приведена формула, по которой определяется СКО.
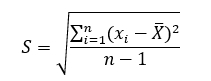 (1)
(1)
где 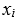 – результат измерения под номером I;
– результат измерения под номером I;
n - число измерений;
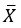 - среднее арифметическое значение результатов n измерений.
- среднее арифметическое значение результатов n измерений.
Эксперимент
Эксперимент проведён при температуре окружающей среды 24 °С. Длительность эксперимента составила 7 минут 44 секунды. Нагрев линзы производился в течение 44 секунд, оставшиеся 7 минут линза остывала.
На рисунке 2 представлена экспериментальная установка, включающая в себя интерферометр, расширитель, источник мощности и сам объект исследования.

Рисунок 2 – Экспериментальная установка
На рисунке 3 более детально показан объект исследования в условиях эксперимента: пленочный нагреватель, при помощи которого произведен нагрев линзы; закрепление типа “плавающий патрон”, в котором очень точно регулируется положение опорных стоек, что позволяет снять с линзы более чёткую интерференционную картину и сам объект исследования – линза.

Рисунок 3 – Экспериментальная установка
Результаты эксперимента представлены в виде интерферометрических изображений, представленных на рисунках ниже, и автоматически рассчитанным СКО, представленным в таблице:

Рисунок 4 – Интерферометрическая картина на 15 секунде остывания

Рисунок 5 – Интерферометрическая картина на 120 секунде остывания

Рисунок 6 – Интерферометрическая картина на 420 секунде остывания
СКО по рабочей поверхности рассчитывается автоматически программным обеспечением интерферометра и составляет:
Таблица 1 – Результаты эксперимента
| Время, сек | СКО, мкм |
| 15 | 0,235 |
| 120 | 0,123 |
| 420 | 0,077 |
Моделирование эксперимента
В качестве тепловой нагрузки для данной задачи используется тепловой поток, действующий на торцевой поверхности линзы, а теплообмен с окружающей средой определяется естественной конвекцией со всех открытых неизолированных поверхностей линзы. На рисунке 7 приведены граничные условия (далее ГУ) и постановка задачи.
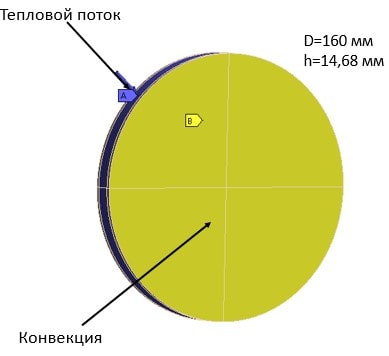
Рисунок 7 – ГУ и постановка задачи
Значения коэффициентов конвекции рассчитаны по общепринятым критериальным уравнениям. Ниже приведён график зависимости значений коэффициента конвекции от разности температур между поверхностью оптического элемента и окружающей средой (рисунок 8).
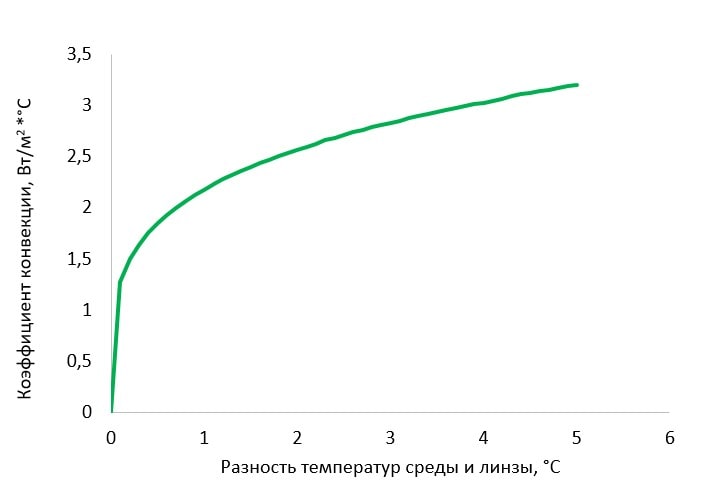
Рисунок 8 – Зависимость коэффициента конвекции от разности температур между поверхностью оптического элемента и окружающей средой
В качестве граничного условия закрепления для оптического элемента используется специальное граничное условие «слабые пружины», которое позволяет реализовать мягкое закрепление оптического элемента в пространстве. Это необходимо для исключения вероятности получения некорректного напряжённо-деформированного состояния оптического элемента в следствии не реалистичного закрепления, которое обязательно повлияет на деформацию рабочей поверхности линзы.
Сравнение результатов математического моделирования и эксперимента
На рисунке 9 представлено типовое распределение поля деформации рабочей поверхности линзы.
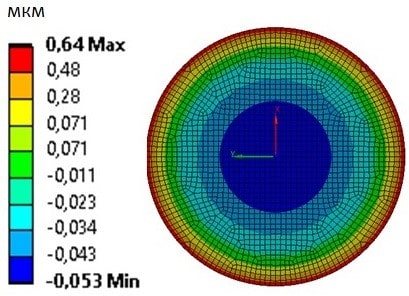
Рисунок 9 – Типовое распределение поля деформации рабочей поверхности линзы, мкм
Сравнение результатов эксперимента и расчётов приведено в таблице 2 ниже:
Таблица 2 – Сравнение результатов эксперимента и моделирования
| Время, сек | СКО, мкм (эксперимент) |
СКО, мкм (моделирование) |
Погрешность |
| 15 | 0,235 | 0,203 | 12% |
| 120 | 0,123 | 0,123 | 11% |
| 420 | 0,077 | 0,054 | 29% |
Заключение
В результате эксперимента установлено, что максимальная температура на рабочей поверхности линзы и её деформация возникают на 15 секунде остывания, локализуются на кромке линзы и равны, соответственно, 31,6 °С и 0,640 мкм. Для данной временной точки расхождение результатов моделирования и эксперимента составляет 13 %. Наибольшее расхождение результата математического моделирования и результата эксперимента соответствует 420 секунде остывания линзы и составляет 29 %.
В результате проведённой работы по отработке разработанной методики установлено, что применение метода конечных элементов является реальным и достаточно эффективным инструментом для определения деформации рабочих поверхностей оптических элементов. При сравнении результатов математического моделирования с результатами натурного испытания установлено, что методика определения деформации рабочей поверхности оптического показывает себя эффективнее при большем градиенте температур между окружающей средой и самим оптическим элементом.

.png)





