Анализ конструкций при нагрузках, приводящих к пластическим деформациям – это то, с чем часто приходится сталкиваться инженерам при проведении расчетов прочности методом конечных элементов. Для точного выполнения подобных расчетов необходимо правильно задавать механические свойства материалов за пределом текучести.

Кривую пластичности для металлов можно получить с помощью эксперимента на одноосное растяжение образца. Выходными данными экспериментальной установки является диаграмма «сила-удлинение». Как эта информация может быть использована для описания поведения материала? Приблизиться к ответу на этот вопрос можно, разделив значения нагрузки на площадь поперечного сечения образца (инженерные напряжения), а значения удлинения - на начальную длину образца (инженерные относительные деформации). На получившейся диаграмме напряжения-деформация можно выделить два характерных уровня напряжений: условный предел текучести (или просто предел текучести), а также предел временного сопротивления (или предел прочности).

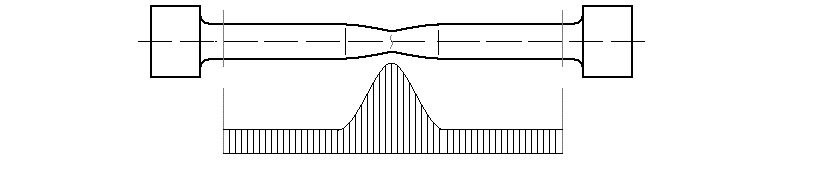
Участок диаграммы от предела текучести до предела прочности называется зоной упрочнения. Напряжения будут продолжать увеличиваться с ростом деформаций до тех пор, пока упрочнение будет компенсировать уменьшение площади поперечного сечения образца. Когда компенсация прекращается в точке предела прочности, последующее растяжение образца сопровождается уменьшением растягивающей силы, вплоть до разрушения образца. Экстремум на кривой соответствует пределу прочности, который возникает в связи с геометрическими эффектами, но не описывает актуального напряженного состояния в образце. Деформация за пределом прочности сопровождается образованием шейки на образце и резким уменьшением поперечного сечения. И хотя усилие падает, напряжения на самом деле растут. Необходимо помнить, что это данные, полученные из испытательной машины.

Если информация об актуальном напряженном состоянии важна, например, при моделировании методом конечных элементов, то для описания поведения материала потребуется уточненный подход.  Рассмотрим, как конвертировать экспериментальные данные для их использования при конечно-элементном моделировании.

Уравнения, связывающие инженерные напряжения (engineering stress) и инженерные относительные деформации (engineering strain) с истинными напряжениями и истинные полными деформациями (true stress – true total strain) действительны вплоть до предела прочности. В дальнейшем для того, чтобы получить значения истинных напряжений и относительных деформаций, должна быть измерена площадь сечения образца. Как только материал становится пластичным, дальнейшая деформация образца происходит с незначительными изменениями в объеме (коэффициент Пуассона близок к 0,5).  Это позволяет связать изменение длины с изменением площади сечения образца, в результате чего удается перевести инженерные напряжения и инженерные относительные деформации в истинные напряжения и истинные деформации вплоть до предела прочности с помощью следующих уравнений:

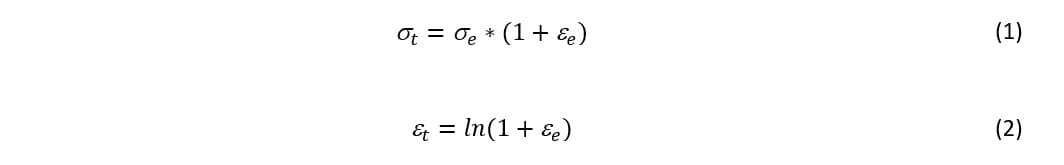
На рисунке ниже показано сравнение диаграмм инженерных и истинных напряжений:

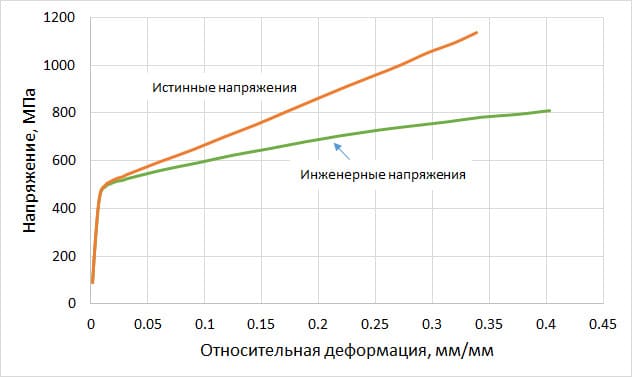
Как правило, программы для прочностных расчетов, в том числе ANSYS, позволяют задавать зависимость «напряжения-относительные деформации» в виде «истинные напряжения – истинные пластические деформации». В таком случае, данные должны быть конвертированы следующим образом:

Модуль упругости (Modulus) = истинные напряжения, в точке, соответствующей значению предела текучести (TrueStress)/истинные полные деформации в этой же точке (TrueStrain).

Далее, нужно перевести инженерные напряжения и инженерные относительные деформации в истинные напряжения и истинные полные деформации, используя формулы (1) и (2). Затем вычесть истинные упругие деформации из истинных полных деформаций в каждой точке, чтобы определить истинные пластические деформации (истинные пластические деформации (TruePlasticStrain) = истинные полные деформации (TrueTotalStrain) – истинные упругие деформации (TrueElasticStrain)).

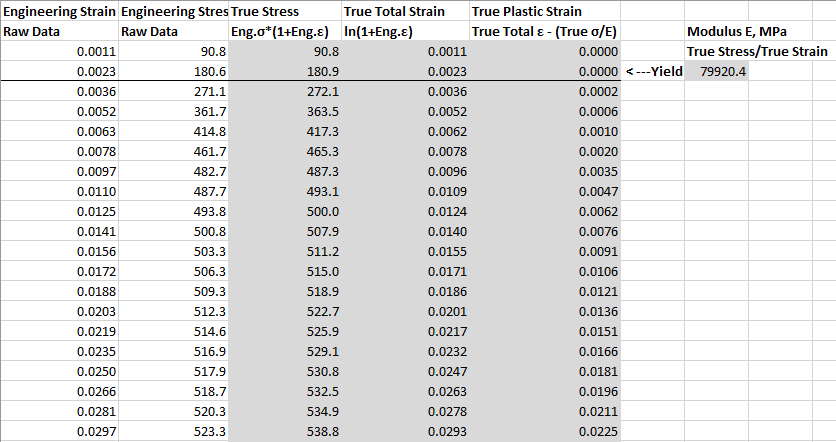
Необходимо помнить следующее при анализе и обработке кривой деформации-напряжения:

1. Прямолинейный участок кривой «истинные напряжения – истинные полные деформации» определяет наклон, или упругую характеристику материала (т.е. на этом участке справедлив закон Гука: Напряжение = Модуль упругости*Деформация)
2. Истинная пластическая деформация находится путем вычитания из значения полной деформации упругой деформации (истинного напряжения, деленного на модуль упругости).
3. Истинная полная деформация в точке, соответствующей значению предела текучести, эквивалентна истинной упругой деформации, а истинная пластическая деформация в этой точке равна нулю.
4. Если программа для прочностного расчета позволяет задать входные данные в виде «истинные напряжения – истинные полные деформации», то первой точкой зависимости должны быть истинное напряжение, соответствующие пределу текучести и истинная полная деформация в этой же точке.
5. Если программа требует ввода входных данных в виде «истинные напряжения- истинные пластические деформации», то первой точкой зависимости должны быть истинное напряжение, соответствующие пределу текучести и истинная пластическая деформация (равна нулю).
6. Зависимость истинных напряжений от истинных деформаций вычисляется вплоть до предела прочности. При моделировании можно предполагать, что при достижении этой точки, материал является абсолютно пластичным (т.е. деформации продолжат увеличиваться без увеличения напряжений). Большинство кодов принимают это предположение по умолчанию.