В инженерной практике в нефтегазовой, аэрокосмической и других отраслях промышленности зачастую возникают задачи расчетов прочности колец уплотнений или резиновых прокладок. В данном обзоре рассмотрены особенности численного моделирования изделий из эластомеров и резины методом конечных элементов.

Для многих материалов линейная модель зависимости напряжения от деформации не описывает их поведение под механической нагрузкой. К таким материалам относится резина, поведение которой можно описать как нелинейно упругое, изотропное, несжимаемое и не зависящее от скорости деформации. Аналогичное поведение демонстрируют вулканизированные каучуки, наполненные эластомеры и даже биологические ткани. Подобные материалы называют гиперупругими.

Гиперупругий материал (упругий материал Грина) – тип модели идеально упругого материала, для которого зависимость напряжений от деформаций вычисляется на основе функции энергии деформации. Гиперупругий материал является частным случаем упругого материала Коши. Роналд Ривлин и Мелвин Муни первыми в 1948 г. разработали математические модели гиперупругого материала – нео-Гуковскую модель и модель Муни-Ривлина. С тех пор был разработан еще ряд моделей, среди которых наиболее широкое распространение получили модель Огдена и Арруда-Бойса.

Кольца уплотнения из резины

По определению, гиперупругий материал является упругим, т.е. нагрузка и разгрузка материала происходят по одной кривой напряжение-деформация. Обычно гиперупругий материал более податлив на растяжение, чем на сжатие, а соотношение между напряжением и деформацией является существенно нелинейным. При воздействии нагрузки на гиперупругий материал объемного сжатия обычно не происходит, т.е. материал ведет себя как полностью несжимаемый, что эквивалентно заданию коэффициента Пуассона равного 0.49 в линейно упругой модели.

Получение практической сходимости численного решения методом конечных при выполнении нелинейного расчета прочности детали из гиперупругого материала может оказаться нетривиальной задачей. Опишем ключевые факторы, которые могут улучшить сходимость и помочь инженеру-расчетчику получить точный результат в обозримые сроки.

1. Проведение тестов материала на растяжение-сжатие

Наличие точных данных испытаний материала является критически необходимым при математическом моделировании изделий из резины и эластомеров. По крайней мере, 2 теста из приведенного ниже списка должны быть выполнены для калибровки модели материала:

• одноосное растяжение
• одноосное сжатие
• двухосное растяжение
• плоский сдвиг
• объемное сжатие

Данные тестов должны как можно точнее соответствовать материалу изделия (in situ), поскольку процесс изготовления детали (например, методом литья под давлением) может оказать существенное влияние на ее механические свойства.

2. Выбор математической модели материала

Поведение гиперупругого материала может быть описано с помощью одной из распространенных математических моделей – Муни-Ривлина, Огдена, Блатца-Ко, Арруда-Бойса. Выбор наиболее подходящей модели может оказать существенное влияние на успех расчета. Наиболее общая рекомендация – выбирайте ту модель материала, которая лучше всего описывает экспериментальные данные в ожидаемом диапазоне деформаций. Выбор модели материала может быть осуществлен методом проб и ошибок, где в качестве критериев фигурируют точность описания экспериментальной кривой и скорость сходимости решения. Рекомендуется начинать исследование с наиболее простой двухпараметрической модели Муни-Ривлина и следить за уровнем деформаций в решаемой задаче. Например, если деформации в задаче не превышают 30%, то нет необходимости добиваться соответствия экспериментальной кривой и математической модели в диапазоне до 200%. Некоторые программы конечно-элементного анализа содержат функции автоматического подбора коэффициентов модели материала под экспериментальную кривую.

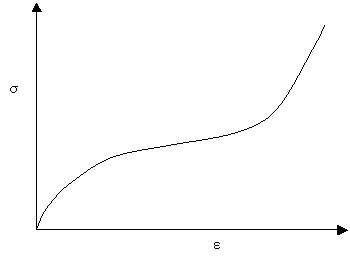
Типичная кривая деформирования гиперупругого материала

3. Тестирование выбранной модели.

Для определения робастности (устойчивости) выбранной модели материала с заданными коэффициентами рекомендуется выполнить тестовое виртуальное нагружение одного конечного элемента. На трех ортогональных гранях элемента ставятся условия симметрии, а на одной из свободных граней задаются конечные перемещения. Задание кинематических граничных условий (перемещений) обеспечивает быструю и устойчивую сходимость решения. Полученные результаты необходимо сравнить с данными экспериментального нагружения, выполнив перевод деформаций из условных в истинные. Сравнение скорости сходимости для различных моделей материала может оказаться решающим факторов при выборе в пользу той или иной модели, для обеспечения экономии процессорного времени.

4. Формулировка конечных элементов

Выбор корректной численной формулировки конечных элементов может оказать критическое влияние на точность и скорость получения решения, особенно при сжатии эластомеров, когда проявляются численные эффекты запирания (locking) конечных элементов. Коммерческие программы могут предлагать различные формулировки элементов, наиболее распространенными из которых являются следующие:

• Выборочно-сокращенное интегрирование (Selective Reduced Integration) для преодоления проблемы запирания элементов;
• Сокращенное интегрирование (Uniform Reduced Integration) для ускорения времени расчета;
• Улучшенная формулировка деформации (Enhanced Strain Formulation) для уточнения поведения при изгибе элементов низших порядков путем введения дополнительных «внутренних» степеней свободы;
• Смешанная формулировка перемещение-давление (u-P) для преодоления проблемы запирания элементов путем введения дополнительной степени свободы – гидростатического давления.

5. Сеточное разбиение

При анализе поведения гиперупругих материалов форма элементов в деформированном состоянии детали после приложения нагрузки играет более важную роль, чем форма элементов в исходном состоянии. Начальное сеточное разбиение необходимо планировать исходя из ожидаемых деформаций. Элементы более низкого порядка ведут себя численно более устойчиво, зачастую для уменьшения искажения формы рекомендуется применять треугольные и тетраэдральные сетки. Измельченная сетка не всегда является лучшей в задачах с гиперупругими материалами, поскольку мелкие конечные элементы в зонах высоких деформаций испытывают большие искажения формы. В случае невозможности достичь сходимости, но не ранее чем применены иные способы улучшения модели, рекомендуется применять адаптивное перестроение сетки.

6. Контроль нагружения

Рекомендуется применять кинематическое нагружение (граничные условия – перемещения) и разбивать приложение нагрузки на большое количество подшагов, поскольку накопление невязок при больших временных шагах может явиться причиной отсутствия сходимости решения.