В статье рассмотрены особенности проведения гармонического анализа колебаний конструкций на примере вращающегося вала с дисбалансом.
Данная статья является адаптированным переводом материала https://caeai.com/blog/harmonic-response-analysis-phase-angle-relationships.
Вибрация – это механические колебания тела или конструкции. Колебания могут быть вызваны как внешним воздействием с определенной частотой возбуждения, так и наличием собственных частот в конструкции. Если частота возбуждения близка к собственной частоте конструкции, то тело войдет в состояние, которое называется резонансом. Данный эффект характеризуется увеличением амплитуды вибрации и фазовым сдвигом между входной нагрузкой и откликом.
В статье рассматривается вращающийся подвесной вал с дисбалансом, изображенный на рисунке 1 вместе с формами колебаний на первых двух собственных частотах.
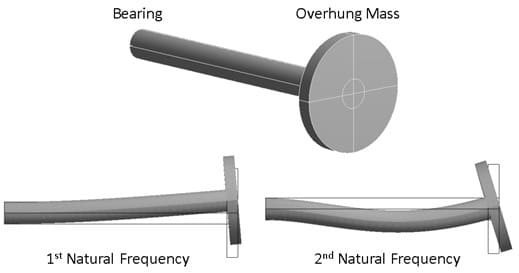
Рисунок 1 – Исследуемый объект. Формы колебаний
Измерение амплитуды свободного конца вращающегося вала при возрастающей скорости вращения от 0 до 300 Гц будет выглядеть так, как показано на рисунке 2. Пиковые значения амплитуд (отмечены серыми линиями) показывают наличие двух собственных частот. В этих областях частота вращения совпадает с собственной частотой колебания, вызывая не только увеличение амплитуды колебания не закрепленного конца вала, но и фазовый сдвиг отклика конструкции.

Рисунок 2 – Амплитудно-частотная характеристика свободного конца вала
Характеристика Phase на рисунке 2 описывает фазовый сдвиг отклика системы относительно входной нагрузки. При детальном рассмотрении первого экстремума (рисунок 3) для скоростей вращения вала, намного ниже собственной частоты, фазовый сдвиг почти равен нулю. Например, при скорости вращения вала, близкой к нулю (<<1 Гц), направление действия нагрузки будет совпадать с направлением перемещения вала и соответствовать статическому отклику. По мере того, как частота вращения вала увеличивается, она приближается к собственной частоте колебания вала, а отклик системы от входной нагрузки начинает отставать. В конечном итоге частота вращения сравняется с собственной частотой колебания вала, система войдет в резонанс и произойдет фазовый сдвиг: отставание отклика системы от входной нагрузки будет максимальным. В классическом примере с одной степенью свободы фазовый сдвиг при резонансе составляет 90°.
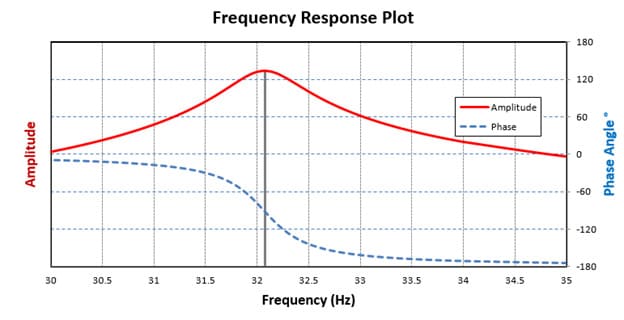
Рисунок 3 - График частотной характеристики вблизи резонансной частоты
Сдвиг по фазе проиллюстрирован на рисунке 4. Если смотреть вдоль оси вала, то плоскость XY и фазовый сдвиг показаны из исходного положения эксцентрической нагрузки при 0°. На диаграмме «Input load position angle 0°» показано мгновенное положение входной нагрузки на валу (отмечена серым маркером, находится в положении 0°). Каждая последующая диаграмма показывает, как изменяется со временем положение входной нагрузки (показаны углы положения нагрузки 90°, 180° и ‑90°).
Все остальные цветные маркеры показывают отставание максимального отклика при различных скоростях вращения вала. Синий маркер показывает результат расчета в статической постановке «околонулевая скорость», а его положение показывает положение входной нагрузки при перемещении вокруг вала. В такой постановке, при низкой скорости вращения, отклик не имеет задержки по фазе. Когда скорость вращения вала увеличивается и приближается к собственной частоте (красный маркер), отклик начинает отставать от входной нагрузки. Если скорость продолжит увеличиваться, приближаясь к собственной частоте, отставание по фазе продолжит увеличиваться. Также, обратим внимание, что максимальный сдвиг по фазе, который составляет 90°, возникает тогда, когда частота вынужденных колебаний совпадет с собственной частотой колебаний.
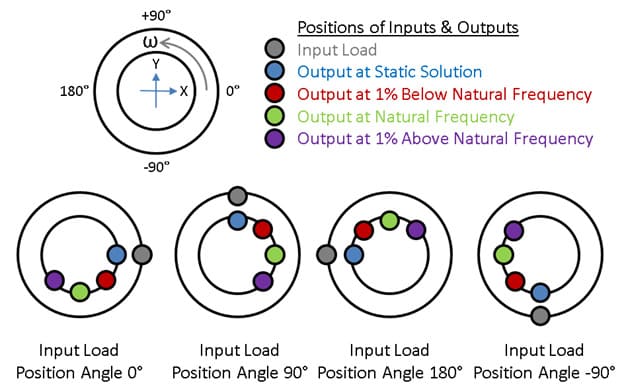
Рисунок 4 - Поведение системы
Этот непрерывный фазовый сдвиг дополнительно проиллюстрирован на рисунке 5, если взглянуть на конкретный компонент перемещения, например, в направлении X, свободного конца вала. «Статический» отклик (синяя линия) с низкой частотой вращения на рисунке 5 показывает, что разница между нагрузкой, подаваемой на входе, и откликом пренебрежимо мала. Если частота вращения чуть ниже (на 1%) собственной частоты то, отклик на валу сдвигается от входной нагрузки на 45° (красная линия). На собственной частоте сдвиг отклика на валу от входной нагрузки составляет 90° (зеленая линия) и на 130° с частотой, превышающей собственную частоту на 1% (фиолетовая линия). Если бы это была система с одной степенью свободы, фазовый сдвиг асимптотически приближался бы к 180° по мере увеличения скорости вращения.
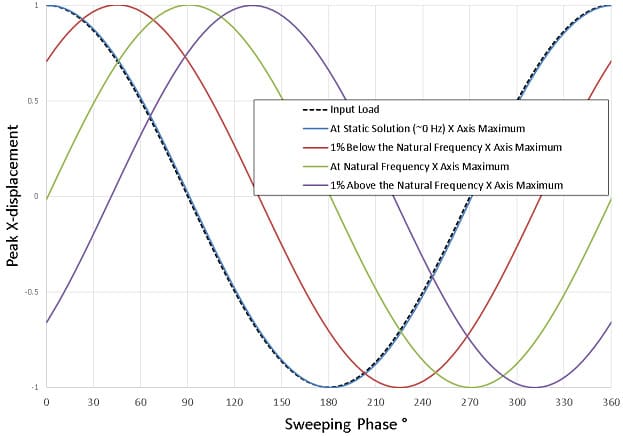
Рисунок 5. Отклики системы при различном сдвиге фазового угла
Теперь, если собрать все вместе (рисунок 6), легко увидеть, как график частотной характеристики связан с откликом системы.

Рисунок 6 - Составная иллюстрация системы валов
Данное объяснение добавляет ясности в части фазового сдвига в гармоническом анализе при резонансе и объясняет, почему мы видим отставание отклика системы при резонансе относительно входной нагрузки, что может казаться нефизичным.

.png)





