Расчет прочности колеса согласно правилам ЕЭК ООН №124 «Единообразные предписания, касающиеся официального утверждения колес для легковых автомобилей и их прицепов» заключается в проведении расчета колеса на косой удар, изгиб при кручении и изгиб при качении.
Данный документ применим для новых сменных колес, предназначенных для транспортных средств следующих категорий:
- M_1, M_1 G- легковые автомобили и легковые автомобили повышенной проходимости соответственно
- N_1, N_1 G- фургоны, предназначенные для перевозки грузов, имеющих полную массу не более 3,5 тонн, и фургонов повышенной проходимости соответственно
- O_1 и O_2 – фургоны, полная масса которых не превышает 0,75 тонн, и соответствующих фургонов повышенной проходимости.
Прочностной расчет колеса позволяет производителям транспортных средств создавать более безопасные и надежные продукты. Также это позволяет конструкторам и инженерам оптимизировать конструкцию колеса, чтобы уменьшить вес или улучшить аэродинамику.
Прочность колеса можно оценить не только по результатам проведения натурного эксперимента, но и при помощи виртуального эксперимента (например, конечно-элементного моделирования).
В ходе эксплуатации диск колеса может быть подвержен возникновению царапин, трещин или вмятин (рисунок 1) вследствие езды по неровным дорогам или же столкновения с различными препятствиями. Царапина или небольшая трещина станет причиной коррозии диска, более крупная трещина может привести к довольно быстрой утечке воздуха или почти сразу же выпустить воздух из шины. Возможно и то, что диск погнётся или даже сломается вследствие ДТП. 
Рисунок 1 – Вмятины на диске колеса и образовавшаяся коррозия
В данной работе объектом исследования является колесо легкового автомобиля. В данной статье мы рассмотрим расчётные случаи, касающиеся прочностного расчета колеса:
- расчет диска колеса на косой удар;
- изгиб при кручении;
- изгиб при качении.
Геометрическая модель диска
Диск представляет собой литую конструкцию, его геометрическая модель представлена на рисунке 2. 
Рисунок 2 – Конструкция рассматриваемого диска
Расчет на изгиб при кручении
Согласно приложению 6 ЕЭК ООН №124 в ходе испытания на изгиб при кручении имитируются поперечные силы, воздействующие на колесо при движении автомобиля по кривой. Обод колеса жестко закрепляется, а в зоне крепления колеса к ступице прилагается изгибающий момент, вычисляемый по следующей формуле:
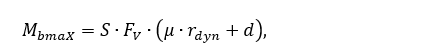(1)
где 
– коэффициент запаса прочности;
– максимальная несущая способность колеса;
– коэффициент трения;
– динамический радиус самой большой шины;
– вылет колеса.
Критерий прочности при расчете на изгиб при кручении – число циклов до разрушения.
Граничные условия и нагрузки при расчете кручения колеса представлены на рисунке 3.
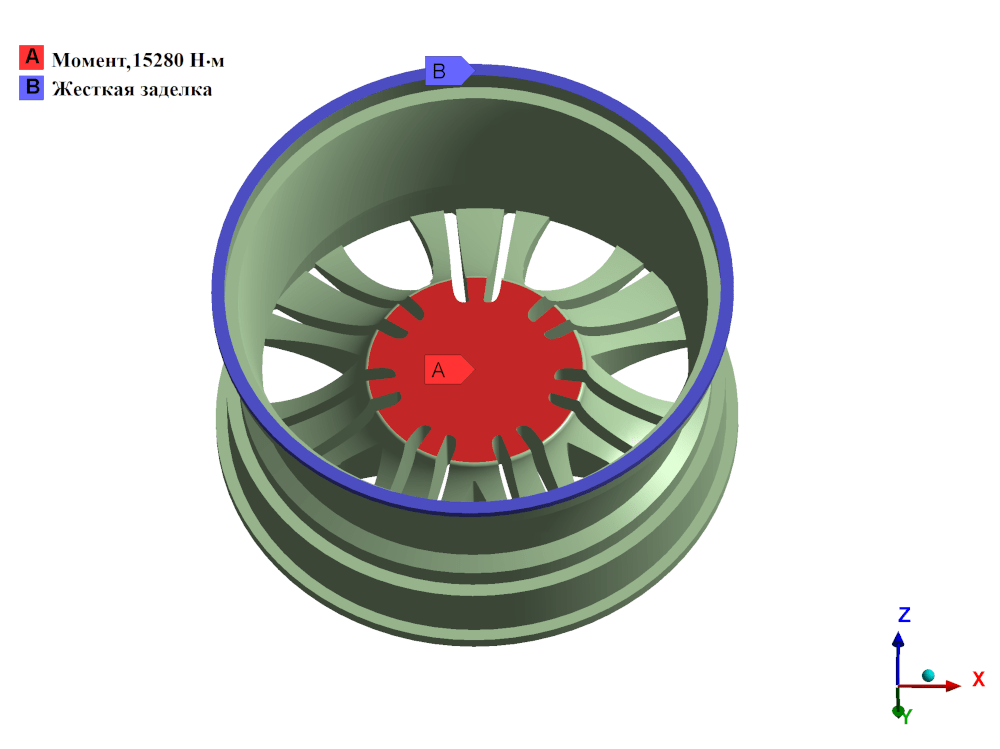Рисунок 3 – ГУ и нагрузка при расчете на кручение колеса
Расчет при качении
Согласно приложению 7 ЕЭК ООН №124 в ходе испытания при качении имитируется напряжение, возникающее в колесе при движении транспортного средства по прямой, посредством вращения колеса. Зона крепления колеса к ступице жестко закрепляется, по ободам действует испытательная нагрузка (сила), к внешней поверхности колеса приложено давление, имитирующее давление воздуха в шине.
Испытательная нагрузка вычислена по следующей формуле:
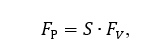(2)
где – коэффициент запаса прочности;
– максимальная несущая способность колеса.
Критерий прочности при расчете при качении – число циклов до разрушения.
ГУ и нагрузки при расчете на качение представлены на рисунках 4 – 5.
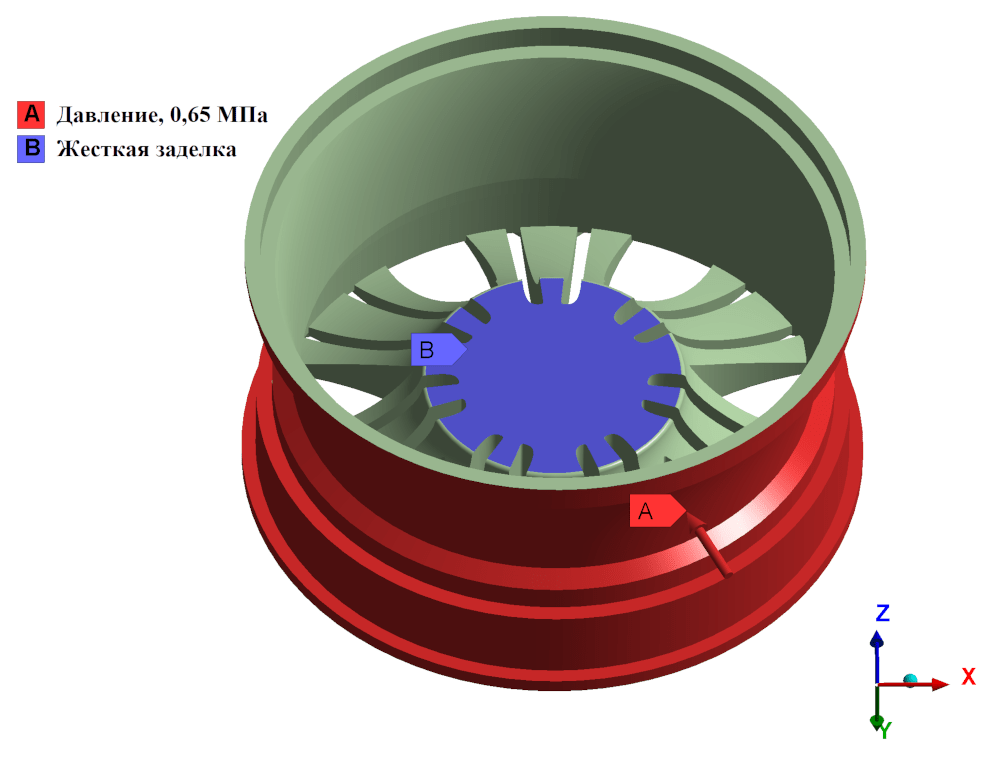Рисунок 4 – Жесткое закрепление и приложенное давление при расчёте при качении колеса
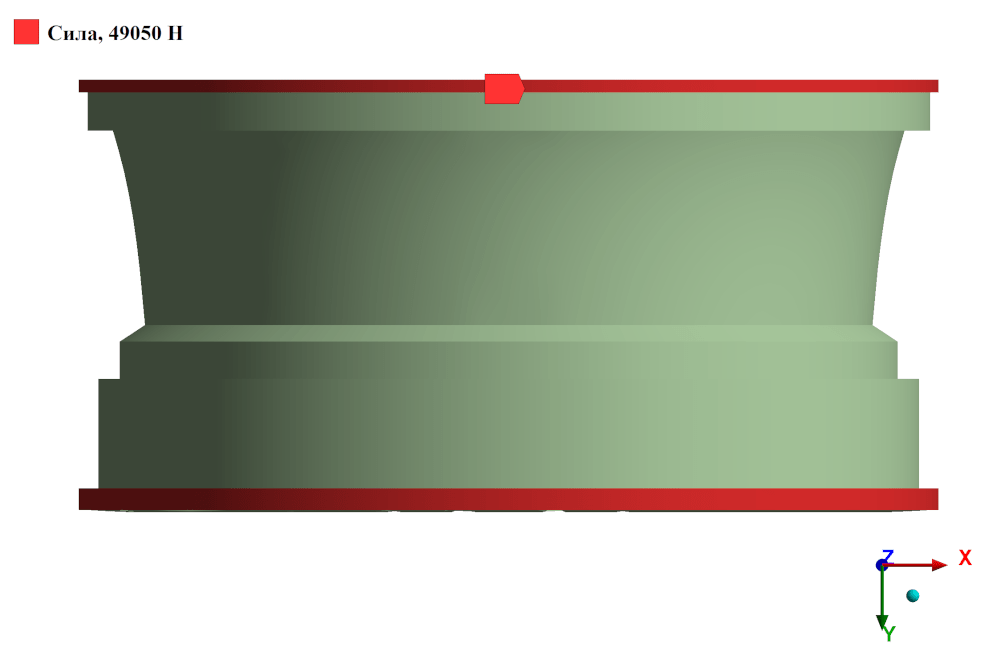
Рисунок 5 – Приложенная перерезывающая сила при расчете колеса при качении
Расчет на косой удар
Согласно приложению 8 ЕЭК ООН №124 в ходе испытания на косой удар проверяется прочность колеса на разлом на закраинах и в других критических точках при ударе колеса о препятствие. При проведении испытания на диск, закреплённый под углом 13° относительно вертикали, свободно падает ударный элемент, что позволяет имитировать потенциальный удар колеса о препятствие. Масса падающего груза вычислена по следующей формуле:
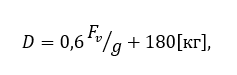(3)
где 
– масса груза, кг;
– ускорение свободного падения, мм/с2.
Скорость груза перед ударом вычисляется по следующей формуле:
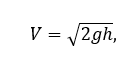(4)
где 
– скорость перед ударом, мм/с;
– высота падения ударного элемента, отсчитываемая относительно высшей точки бортовой закраины диска и равная 230 мм.
На рисунке 6 представлена постановка задачи при расчете на косой удар.
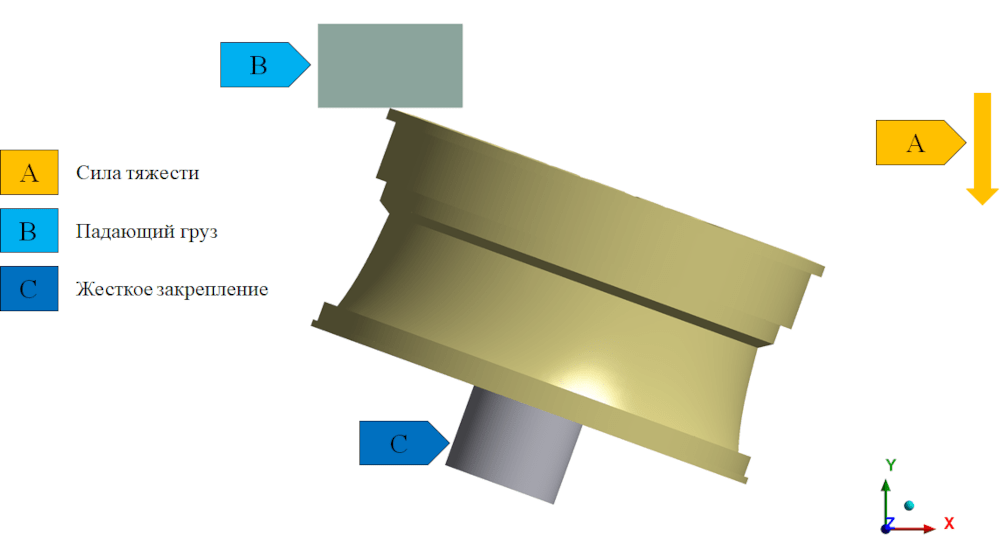Рисунок 6 – Постановка задачи на косой удар
Результаты расчетов
Расчет на изгиб при кручении
Распределение эквивалентных напряжений по Мизесу представлено на рисунке 7. Из рисунка видно, что максимальные напряжения возникают в местах соединения спиц диска с ободом и ступицей соответственно. Максимальные напряжения, возникающие в диске при проведении испытания, не превышают предел временного сопротивления, равный 
= 294,3 МПа.
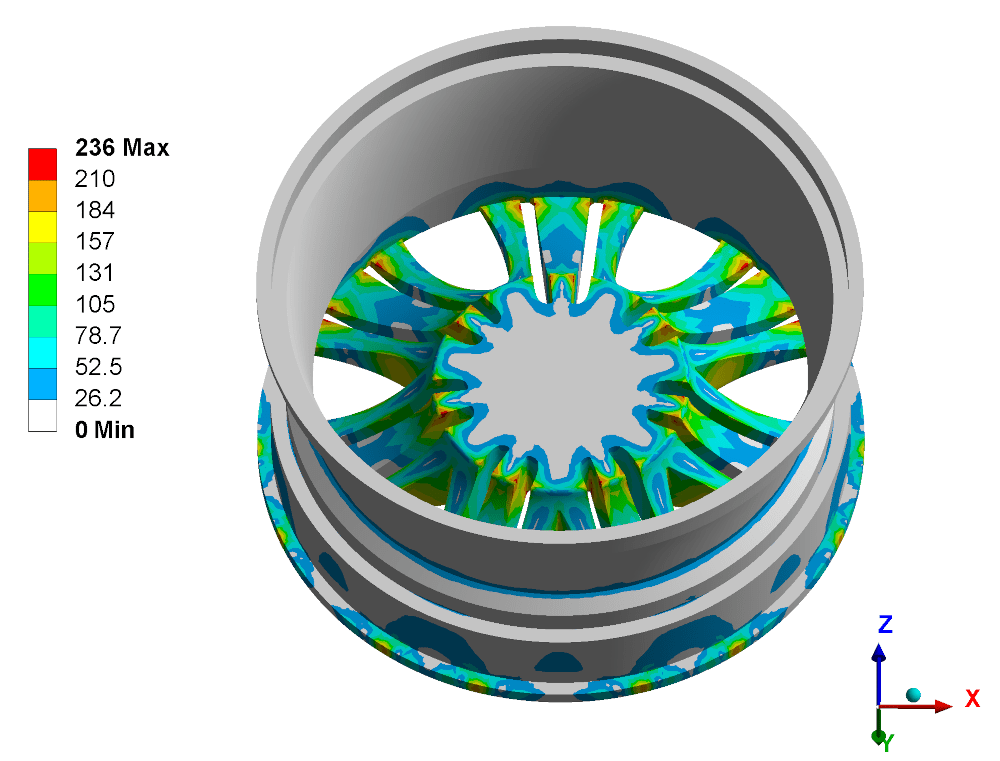Рисунок 7 – Распределение эквивалентных напряжений по Мизесу при испытании на изгиб при кручении, МПа
Количество циклов до разрушения при нагружении 75% 
приведено на рисунке 8.
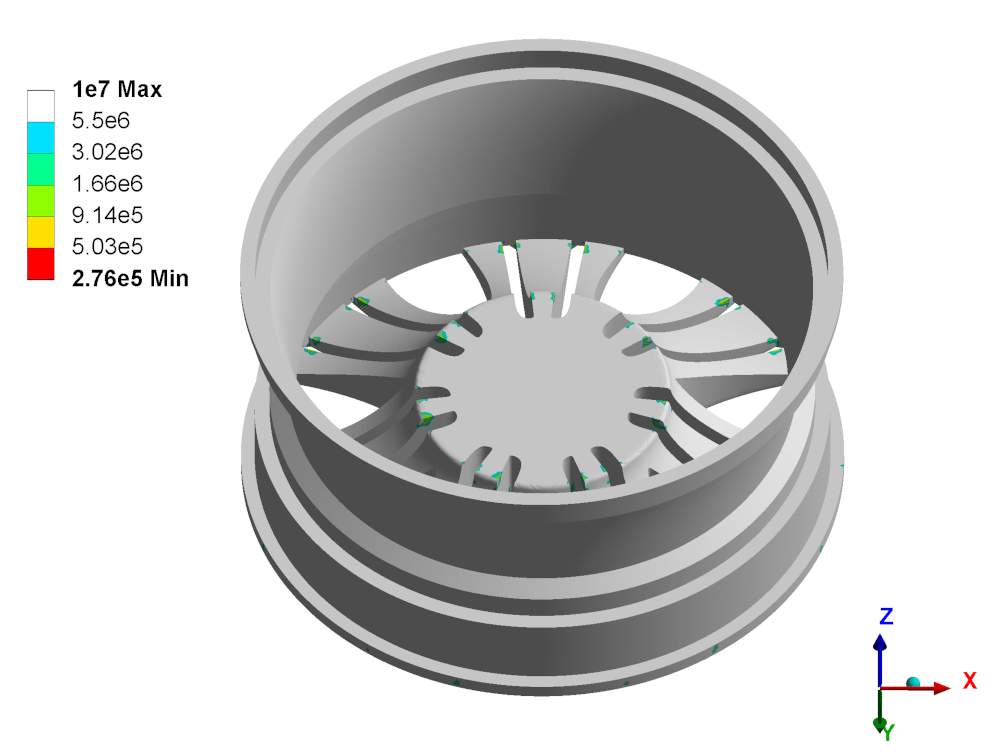Рисунок 8 – Распределение количества циклов до разрушения для 75% при испытании на изгиб при кручении
Конструкция колеса проходит испытание на изгиб при кручении, так как количество циклов до разрушения больше, чем 200000 для 75% (для ТС категорий M1, M1G, являющихся нестальными конструкциями)
Расчет на качение
Колесо удовлетворяет испытанию на качение, если число циклов до разрушения не менее:
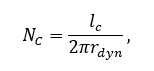(5)
где 
– требуемый в испытании эквивалентный пробег, принимаемый равным 2000 км для колёс не из стали;
– динамический радиус самой большой шины, принимаемый равным 366 мм.
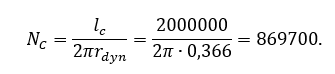(6)
Распределение эквивалентных напряжений по Мизесу представлено на рисунке 9.
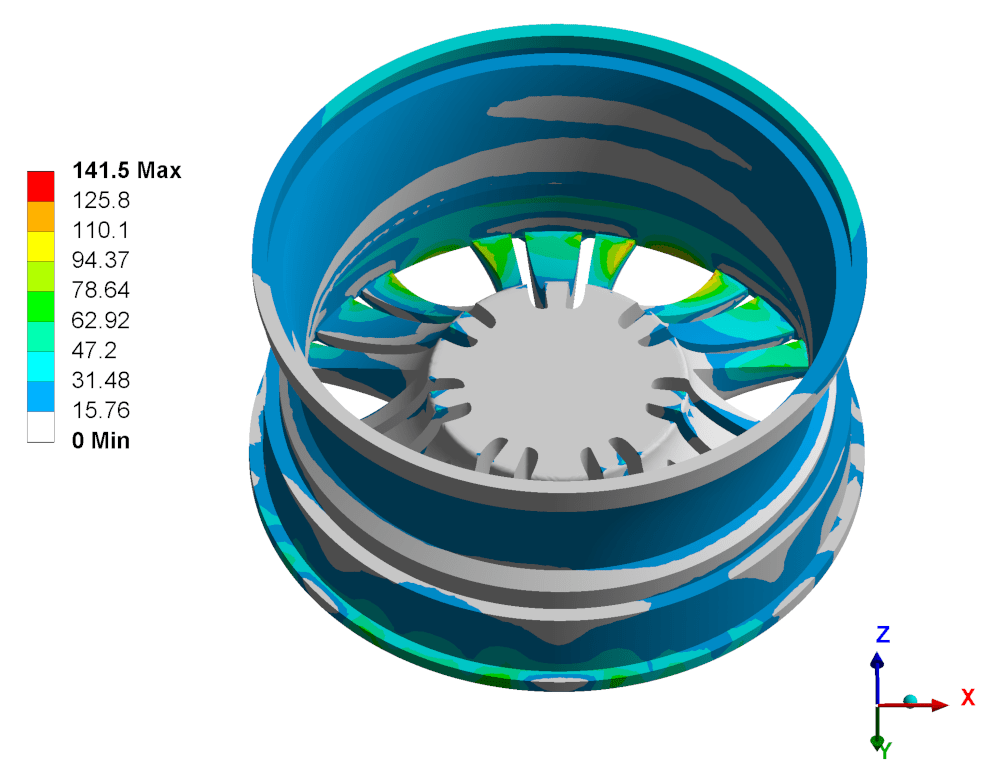Рисунок 9 – Распределение эквивалентных напряжений по Мизесу при испытании на изгиб при кручении, МПа
В соответствии с кривой Велера, характеризующей поведение материала при циклическом нагружении и приведенной на рисунке 10, получено распределение количества циклов до разрушения, представленное на рисунке 11.
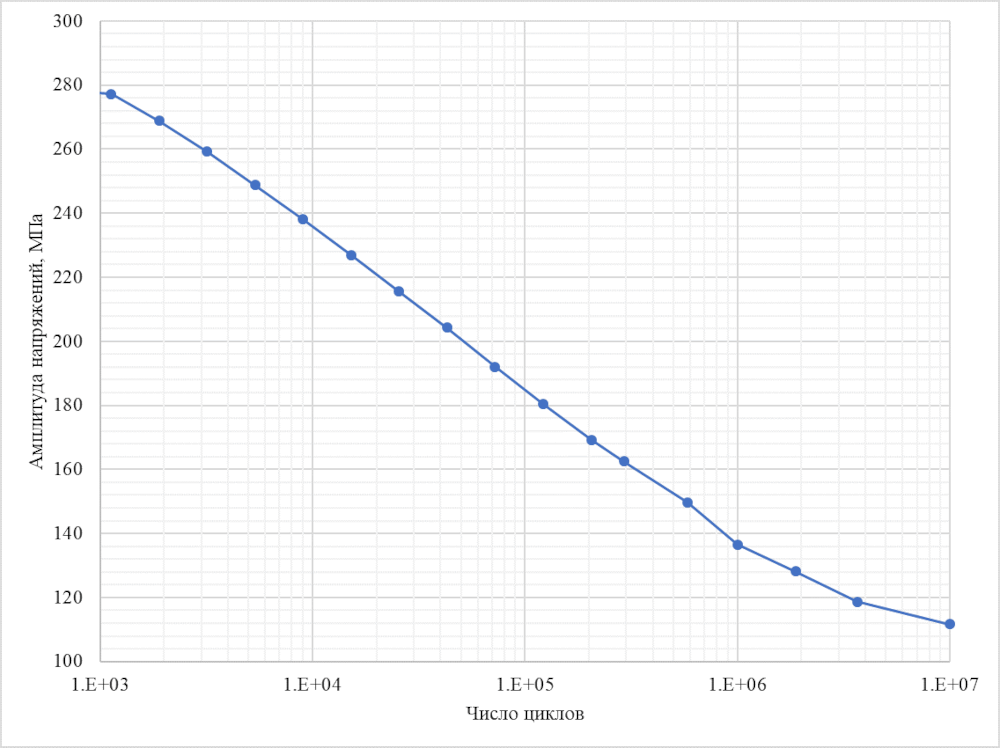Рисунок 10 – Кривая Велера для материала диска
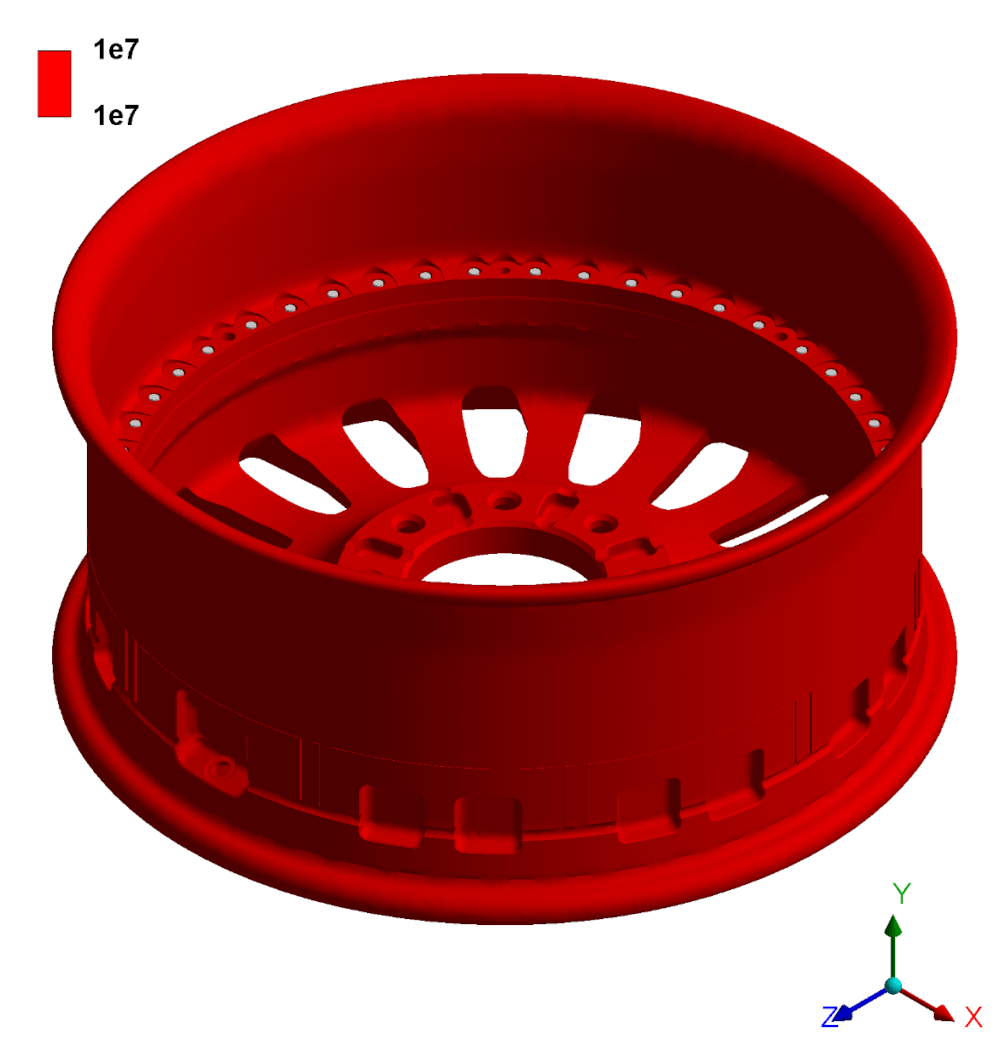Рисунок 11 – Распределение количества циклов до разрушения при испытании на качение
Из результатов рисунка 11 можно сделать вывод, что прочностной расчёт при качении пройден успешно, так как количество циклов до разрушения больше, чем 
=869700, определённому согласно формуле (6).
Результаты расчета на косой удар
В данном расчете оценивается возможность появления сквозных трещин в центральном элементе колеса.
Колесо удовлетворяет испытанию на косой удар если приведенные напряжения не превышают предела временного сопротивления ( = 294,3 МПа).
На рисунке 12 приведено распределение приведенных напряжений во всем колесе.
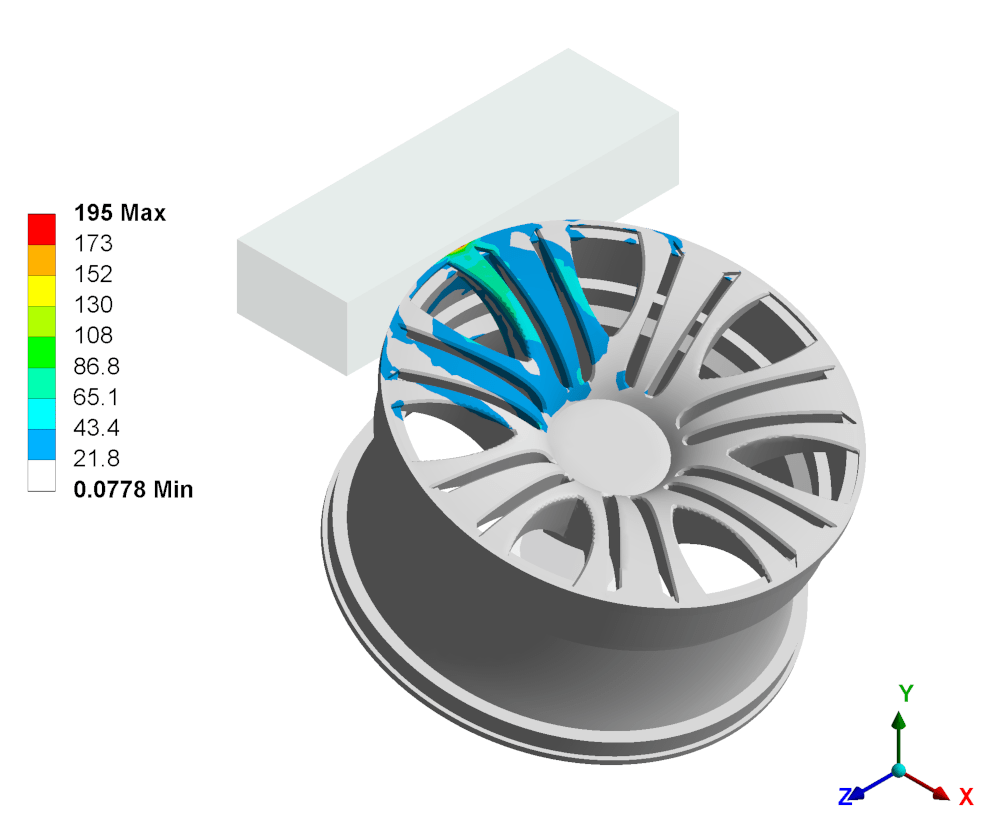Рисунок 12 – Распределение приведенных напряжений во всем колесе при расчете на косой удар, МПа
Из рисунка 12 видно, что максимальное напряжение в колесе при расчете на косой удар не превышает предел временного сопротивления, следовательно, разрушения, согласно Правилам ЕЭК ООН №124, не наблюдается
Заключение
В прошлом для проведения прочностных расчетов колес ставились натурные опыты. С развитием технологий появилась возможность проводить такие расчеты в программных комплексах, использование которых позволяет снизить денежные затраты за счет отказа от натурного эксперимента, а также дает возможность корректировки геометрии колеса в процессе его оптимизации.
Наша компания может провести прочностной расчет колеса, а в случае несоответствия данного колеса прочностным критериям и его геометрическую оптимизацию.
