Во многих случаях разрушения элементов конструкций и оборудования важную роль играет механизм разрушения, вызванный явлением ползучести материала. Так, например, явление ползучести металла при высоких температурах явилось одной из причин разрушения башен-близнецов в Нью-Йорке. Ползучесть также была названа причиной обрушения крыши в Бостонском тоннеле "Big Dig".
Ползучестью называют явление непрерывной пластической деформации материала под действием постоянного напряжения в течение определенного времени. Поведение материала при ползучести обладает следующими свойствами:
- деформация при ползучести, как и при пластичности, является необратимой (неупругой);
- поведение материала при ползучести несжимаемое, т.е. шаровой тензор деформации ползучести равен нулю;
- деформации ползучести появляются при любых ненулевых напряжениях;
- в кристаллических материалах, в том числе в металлах, механизм ползучести связан с микро-механическими явлениями, такими как миграция вакансий и движение дислокаций в кристаллической решетке;
Ползучесть обычно описывается законом зависимости скорости деформации от напряжения, деформации, времени и температуры:
В большинстве материалов при действии постоянной нагрузки выделяют три стадии ползучести. На первой стадии скорость деформации уменьшается со временем. Это явление наблюдается в течение короткого периода времени. Вторая стадия, более длительная, характеризуется постоянным значением скорости деформации. На третьей стадии скорость деформации быстро увеличивается вплоть до полного разрушения материала (разрыва образца).

При решении задачи моделирования ползучести методом конечных элементов получение близкого к точному и сошедшегося решения может представлять трудность, поскольку задача является существенно физически нелинейной. Приведем основные факторы, позволяющие расчетчику получить адекватное решение в обозримый срок.
1. Экспериментальное исследование материала
Наличие точных экспериментальных данных для образца материала является важнейшим фактором успешного решения задачи численного моделирования ползучести. Калибровка математической модели материала по результатам эксперимента подразумевает выбор численно устойчивой модели материала для диапазона деформаций, ожидаемого в рамках данной задачи, и коэффициентов данной модели. Для проведения калибровки требуются экспериментальные данные о зависимости деформации или скорости деформации от времени, и, также, от напряжений и температуры. Анализ чувствительности параметров модели и сравнение полученной кривой с экспериментальными данными позволит выбрать модель материала, дающую наиболее адекватные результаты.
Экспериментальные данные должны как можно точнее соответствовать материалу изделия (in situ), расчет которого необходимо провести. Поскольку процесс деформации при ползучести происходит в течение долгого времени, то тесты материала в реальных условиях эксплуатации чаще всего нереализуемы. Проведение подобного теста может быть ускорено за счет повышенных уровней напряжений и/или температур. Пример подобной процедуры приведен в статье Farrag, K., "Development of an Accelerated Creep Testing Procedure for Geosynthetics, Part II: Analysis,"Geotechnical Testing Journal, Vol. 21, No. 1, 1998, pp. 38-44,http://dx.doi.org/10.1520/GTJ10423J. ISSN 0149-6115. Предложенная в статье процедура основана на применении временного масштабного коэффициента к кривым деформаций ползучести на повышенных температурах для нахождения мастер-кривой на более длительных промежутках времени.
2. Выбор модели материала
Для моделирования ползучести методом конечных элементов существует целый ряд законов поведения материала – от степенной зависимости скорости деформации от напряжения, известной как «закон Нортона» до более сложных форм с учетом временного или деформационного упрочнения. Грамотный выбор модели материала является важнейшим фактором успеха исследования. Необходимо выбирать модель материала, наиболее точно описывающую экспериментальную кривую на всем известном диапазоне. Следует учесть, что некоторые законы ползучести описывают лишь одну стадию ползучести из трех. Выбор модели материала осуществляется в определенной степени методом проб и ошибок, где факторами правильного выбора являются совпадение кривых и скорость практической сходимости численного решения.
Рекомендуется начинать с более простых моделей, например со степенного закона Нортона:
Некоторые программные системы решения задач МКЭ, например, ANSYS, позволяют произвести полу-автоматическую калибровку материала под экспериментальные данные. Чем больше параметров содержит модель, тем сложнее порой достичь совпадения экспериментальной и модельной кривых. Также количество параметров может влиять на сходимость численного решения.
Зависимость от температуры в уравнении ползучести рекомендуется задавать законом Аррениуса (введением соответствующего множителя в модель):
а не использовать температурные зависимости нескольких коэффициентов, т.к. в последнем случае линейная интерполяция может давать неточные результаты и плохую сходимость
3. Тестирование выбранной модели
Для определения численной устойчивости (робастности) выбранной модели материала с заданными коэффициентами рекомендуется выполнить тестовое виртуальное нагружение одного конечного элемента. На трех ортогональных гранях элемента ставятся условия симметрии, а на одной из свободных граней задается усилие (для моделирования ползучести) или конечные перемещения (для моделирования релаксации напряжений). Сравнение скорости сходимости для различных моделей материала может оказаться решающим факторов при выборе в пользу той или иной модели, для обеспечения экономии процессорного времени.
4. Пошаговое нагружение
От выбора шага по времени зависит скорость и сходимость решения. Рекомендуется разработать стратегию выбора шага по времени на тестовой задаче (это может быть нагружение одного конечного элемента или упрощенная двумерная постановка) и применить ее к полному расчету. Приращение деформации ползучести на каждом шаге необходимо контролировать вручную или программными средствами. Так, например, ANSYS позволяет пользователю установить предельное соотношение приращения деформации ползучести на шаге к упругой деформации. Если данное значение в какой-то момент превышено, то происходит бисекция численного решения и шаг по времени уменьшается.

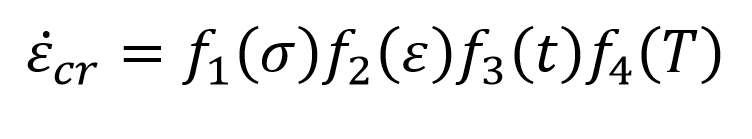
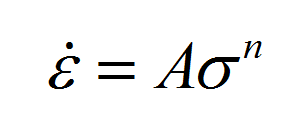
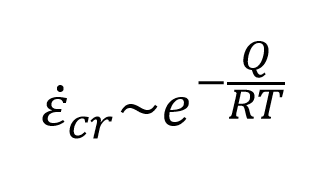
.png)





