В статье рассматриваются подходы к моделированию распространения звука в задачах гидро- и аэроакустики. Особенностью распространения звука в жидких и газообразных средах является наличие конвективных и диссипативных эффектов, что несколько усложняет компьютерное моделирование, поскольку возникает необходимость рассматривать распространение звука и динамику среды совместно.

Помимо гидро- и аэродинамики, задачи акустики встречаются и во многих других областях науки и техники, например: 

• Физиологии и психологии, поскольку органы слуха – это второй основной источник информации о внешнем мире для человека. Исследования особенностей восприятия звука слуховым аппаратом человека необходимо, как для медицины, так и для инженерии. Важно постоянно задумываться о предельных значениях интенсивности звуковых колебаний различных устройств, поскольку у человека существует болевой порог и пределы слышимости. Это актуально в таких задачах, как измерение шума на рабочих местах и оценке его воздействия на человека (ГОСТ ISO 9612-2016).
• При создании электрических устройств для генерации и регистрации звуковых сигналов. Диапазон работы таких устройств не ограничен слышимым спектром человека, подобные устройства применяются в гидрологии, строительстве, медицине и технике. Например, при разработке современных слуховых аппаратов, устройств ультразвуковой диагностики, головных телефонов и т.д.
• В строительстве и архитектуре необходимо задумываться об оптимальном строении различных помещений и объектов для сохранения качества восприятия и распространения звука. В этой области решаются задачи защиты от шума и обеспечения нормативных параметров акустической среды в производственных, жилых, общественных зданиях (СП 51.13330.2011).
• При исследовании объектов, движущихся в воздушной среде. Обычно рассматриваются задачи о возникновении и распространении звуков, создаваемых потоком воздуха или взаимодействие воздуха с движущимся объектом (аэроакустика). Процесс распространения звука в воздухе достаточно сложен, поскольку он осуществляется двумя различными механизмами: распространением волн и переносом вещества. Актуально при оценке уровня шума в салоне и кабине летательного аппарата (ГОСТ 20296-81) или оценке авиационного шума на территории жилой застройки (ГОСТ 22283-88).

В качестве инструмента для моделирования акустики в задачах гидро- и аэродинамики в данном материале использовано специализированное инженерное программное обеспечение Ansys Fluent [1]. Ansys Fluent применяет метод контрольных объёмов для интегрирования уравнений сохранения массы, импульса и энергии (уравнения Навье–Стокса), что позволяет описать механику жидкости и газа и определить основные параметры течения. 

Методы решения задач гидро- и аэроакустики глобально разделяются на прямое акустическое моделирование и гибридные (интегральные) подходы.

Прямое акустическое моделирование

Звук представляет собой распространяющиеся упругие волны в среде, и в случае жидкой среды распространение звуковых волн уже включено в уравнения Навье–Стокса [1], которые описывают движение жидкости или газа. Прямое акустическое моделирование – один из возможных подходов для решения задач гидро- и аэроакустики, по сути, оно представляют собой решение уравнений Навье–Стокса с достаточной степенью точности. При этом в случае численного моделирования существуют некоторые ограничения, препятствующие прямому акустическому моделированию. 

Одним из ключевых параметров в задачах гидро- и аэроакустики является уровень звукового давления, который определяет интенсивность звуковой волны. При этом уровень звукового давления значительно меньше, чем атмосферное давление или давление в потоке жидкости или газа, разница составляет от 5 и более порядков. Энергия звуковых колебаний тоже значительно меньше, чем энергия потока. Это означает, что при численном моделировании необходимо с одинаковой точностью вычислять величины, имеющие такой большой диапазон значений, поэтому требуется чрезвычайно высокая точность расчётов и, соответственно, большие вычислительные ресурсы.

Диапазон частот, воспринимаемых человеческим ухом – от 20 до 20000 Гц, что соответствует длинам волн от нескольких миллиметров до нескольких метров. Для прямого моделирования распространения акустических волн необходимо учитывать распространение даже самых коротких миллиметровых волн, а для этого характерный размер контрольного объёма должен быть меньше, чем длина самой короткой волны. Поэтому резко возрастает общее число элементов в области течения, что значительно увеличивает вычислительные ресурсы. Поэтому прямое акустическое моделирование чаще применяется в исследовательских целях и для задач внутренней акустики, где приёмники сигнала расположены недалеко от источников звуковых колебаний.

Данный подход зачастую применяется для анализа звука, который возникает при обтекании некоторых углублений или полостей. Простейшим примером является пустая бутылка, издающая гул при вдувании в неё воздуха. Это явление называется резонансом Гельмгольца. Этот тип резонанса возникает при нагнетании воздуха в полость, выходя из полости, он заставляет воздух внутри вибрировать с определенной собственной частотой. 

Для иллюстрации применения прямого акустического моделирования в работе проведено моделирование резонатора Гельмгольца по данным эксперимента [2]. Был исследован резонатор, который представляет собой кубическую полость с сечением 50 см х 50 см и высотой 59 см. В верхней части проделано квадратное отверстие 12,5 см х 12,5 см. Толщина верхних стенок 0,1 см. Поток воздуха создаётся при помощи дозвуковой аэротрубы, способной создавать скорость потока до 32 м/с. Микрофон установлен в нижней части полости резонатора. Моделирование проведено в плоской двумерной постановке, для сокращения вычислительных ресурсов.

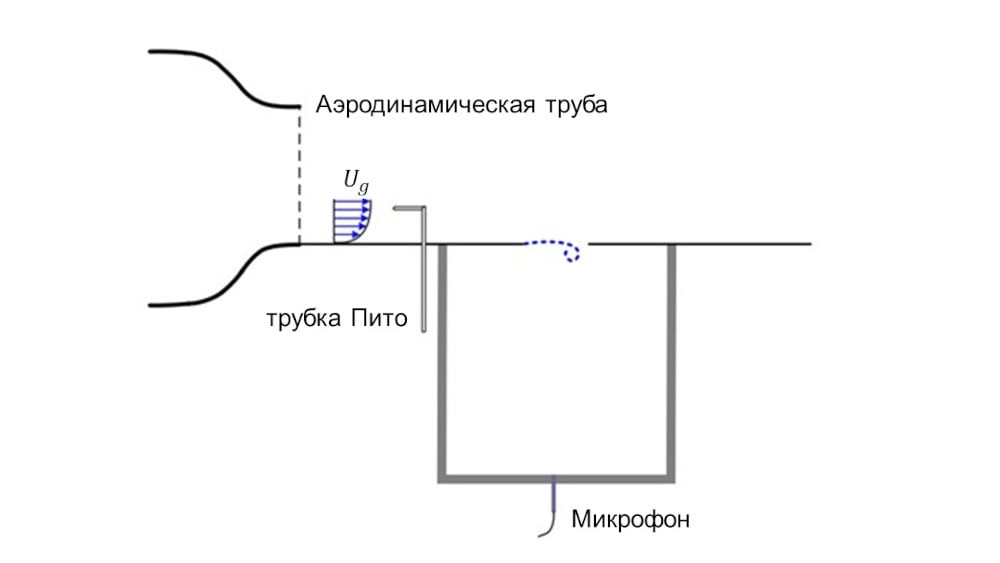Схема резонатора Гельмгольца, исследуемого в эксперименте [2]

Задача решалась в два этапа: стационарный расчёт и нестационарные расчёты. На первом этапе для получения начальных значений проведён стационарный расчёт с использованием SST k–ω модели турбулентности: это означает, что течение считается установившимся, все параметры течения считаются осреднёнными по времени и отсутствуют разного рода флуктуации физических величин.

Поле скорости, полученное при стационарном расчёте

Поскольку звук представляет собой волну и имеет существенно нестационарную природу, то для моделирования распространения звуковых волн на втором этапе проведён нестационарный расчёт. Результаты стационарного расчёта использованы в качестве начальных данных для нестационарного расчёта. Нестационарный расчёт проведён с использованием DES (Detached Eddy Simulation) модели турбулентности для моделирования вихрей.

Поле скорости, полученное при нестационарном расчёте в момент времени t=0.2 с

В ходе моделирования записаны данные о флуктуациях акустического давления в локации микрофона и проведено сравнение временных историй этих флуктуаций с экспериментальными данными.

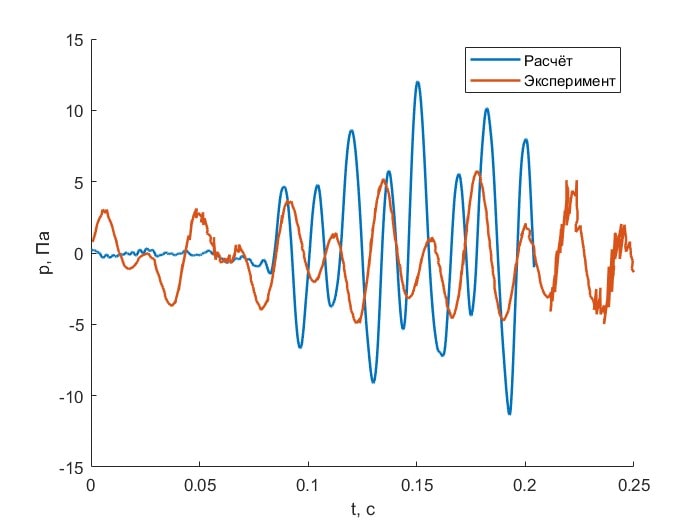Акустическое давление в локации микрофона, сравнение расчётных данных с экспериментом

Заметно качественное совпадение по общей структуре флуктуаций, а также наблюдается совпадение частот колебаний. Важно отметить, что в результате моделирования не учитывались эффекты, связанные с вибрациями самого резонатора. В расчётах оценивается вклад только от вихрей, попадающих в полость резонатора, что может служить причиной расхождения с экспериментальными данными. Для учёта влияния вибраций резонатора необходимо проводить двунаправленный связанный расчёт вычислительной гидрогазодинамики (CFD) и механики твёрдого тела для того, чтобы учесть упругие деформации стенок полости и их взаимодействие с потоком.

Гибридные (интегральные) подходы

Гибридные подходы к моделированию распространения звука позволяют разделить задачи гидрогазодинамики и акустического моделирования.  

Для осуществления таких подходов используется аналогия Лайтхилла [3]. Сложный аэрогидродинамический процесс представляется в виде акустических источников, которые считаются окружёнными однородной покоящейся средой. Таким образом, отдельно решается задача гидро- и аэродинамики внутри некоторой области, граница этой области считается источником звука, а для моделирования распространения звука от источника до приёмника решается однородное волновое уравнение. Результат CFD расчёта является начальным условием для проведения расчётов акустики.

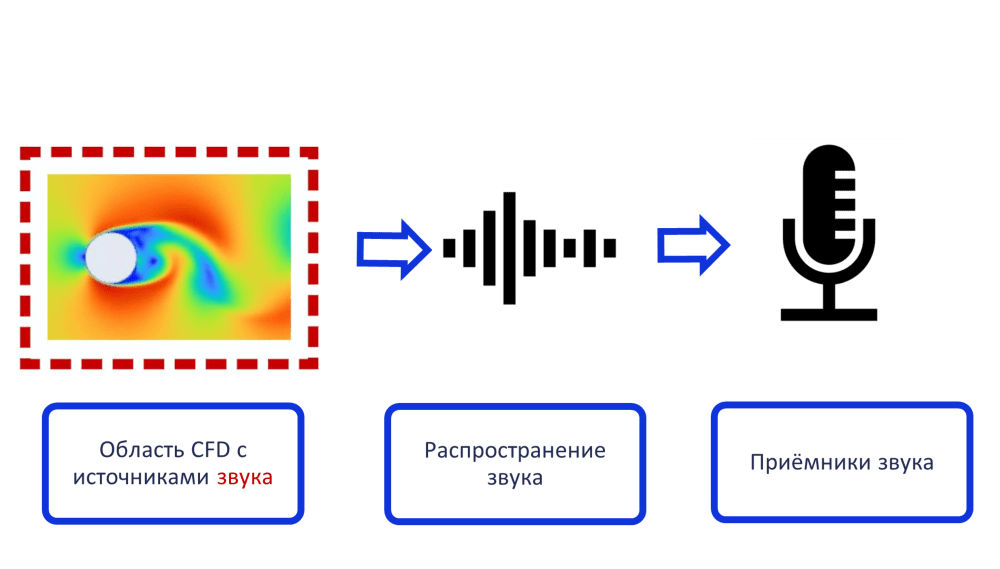Принцип работы гибридных методов

Одна из моделей, реализованная в ПО Ansys Fluent на основе данной аналогии – модель Фокса–Уильямса–Хокинга (FW–H)  [4]. В данной модели уравнение Лайтхилла обобщено на случай движущихся источниковых поверхностей и учитывает конвективные эффекты среды. Данная модель хорошо подходит для моделирования распространения звука на средние и дальние расстояния, однако не может учитывать отражение и/или поглощение звука, поэтому подходит только для моделирования открытых пространств. 

Например, для решения задачи оценки уровня шума, создаваемого выпущенными шасси самолёта [5], отдельно решается задача CFD моделирования внешнего обтекания шасси, затем выделяется источниковая поверхность вокруг области обтекания и решается задача о распространение звука до приёмника, находящегося в заранее заданной точке, на любом расстояние от источниковой поверхности.

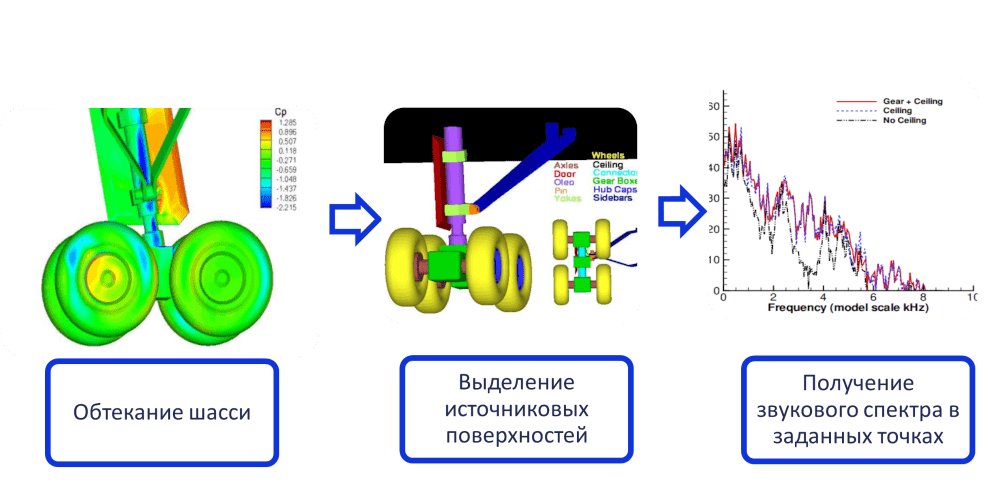Задача оценки уровня шума от шасси. Источник [5]

С помощью модели FW–H определяют акустические данные в конкретных заранее указанных источниках и с помощью преобразования Фурье позволяют вычислять спектр частот. Для моделирования распространения звука используется нестационарный расчёт; шаг по времени выбирается таким образом, чтобы соответствовать максимальной частоте, исследуемой при моделировании. 

Ещё одна интегральная модель, реализованная в ПО Ansys Fluent – модель волнового уравнения (wave equation model в терминологии Ansys Fluent) [5]. Она схожа с моделью FW–H, но не может работать со сжимаемыми течениями. Однако она обладает преимуществом перед моделью FW–H, так как позволяет рассчитывать всё акустическое поле, в то время как FW–H рассчитывает акустический сигнал только в заранее заданных источниках. 

Зачастую во многих задачах нет конкретных источников тонального звука (т.е. звука с определенной частотой), и он генерируется с близким к равномерному распределению по частотам. Часто требуется только оценить общий уровень звукового давления. Для этого применяется модель широкополосного шума (broadband noise model в терминологии Ansys Fluent) [6]. Данная модель основана на полуэмпирических закономерностях, которые используются для решения уравнения Лайтхилла. Она отличается от предыдущих двух моделей, поскольку не моделирует распространение звука, а только оценивает общий уровень звукового давления на границе заданной области.

Для демонстрации возможностей акустического моделирования с помощью гибридных моделей в Ansys Fluent рассмотрена модельная задача протекания жидкости в арматуре: имеется кран, по которому протекает вода с известным массовым расходом.

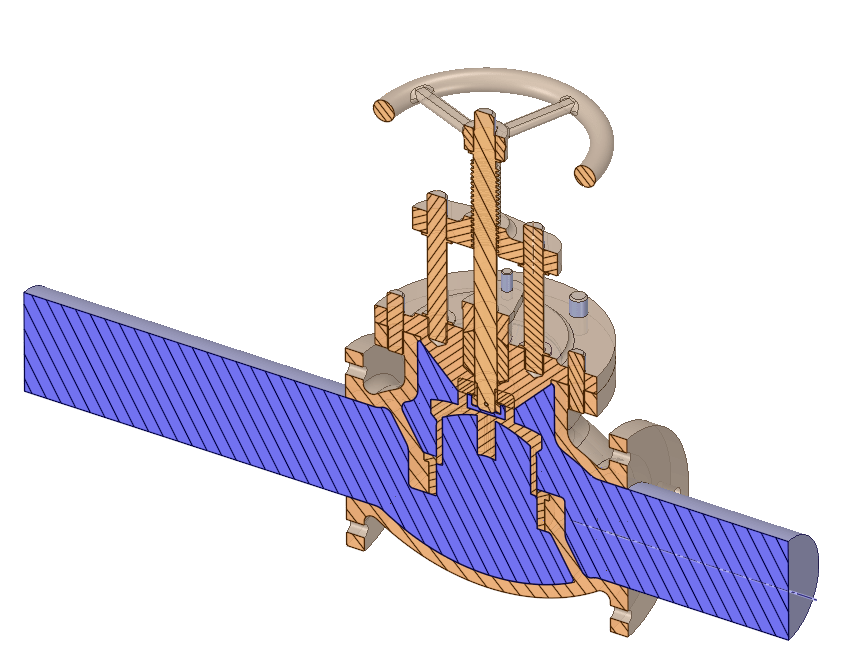Геометрическая модель крана и область течения (выделена синим)

Акустический расчёт проведён с помощью моделей акустики FW–H и модели широкополосного шума. Гидродинамический расчёт проведён с использованием следующих моделей турбулентности: 

• unsteady Reynolds averaged Navier–Stocks (URANS), основанной на осреднении уравнений Навье–Стокса по времени;
• Large Eddy Simulation (LES), основанной на применении пространственного «фильтра» для отделения крупных и мелких вихрей. 

В качестве контрольной поверхности выбрана внешняя поверхность области течения, что соответствует внутренней поверхности крана. 

Уровень акустического давления на поверхности крана

Для модели акустики FW–H установлены локации «приёмников» на расстоянии двух метров от исследуемого крана, в данных точках рассчитывался акустический спектр и уровень звукового давления. Поэтому есть возможно сравнить общий уровень звукового давления для разных моделей турбулентности и акустики. В результате проведённой серии расчётов получены следующие результаты: 

• связка модели турбулентности LES и модели акустики FW–H даёт наибольший уровень звукового давления – 193,5 дБ 
• на 10% больше, чем наибольший уровень звукового давления, полученный при использовании SST k–ω модели турбулентности и FW–H модели акустики (174,7 дБ)
• на 25% больше, чем максимальный уровень звукового давления, полученный при использовании SST k–ω модели турбулентности и модели широкополосного шума (153,0 дБ)

Заключение

Компьютерное моделирование в последние десятилетия стало отличной альтернативой и дополнением к реальным дорогостоящим экспериментам. Оно позволяет создавать цифровые двойники для реальных объектов или описывать различные физические явления. Современное компьютерное моделирование – важный инструмент на различных этапах разработки и оптимизации перспективных устройств, оно позволяет сократить время на проектирование устройств, а также обеспечить безопасность или подтвердить надёжность. На примере рассмотренных задач, можно убедиться, что компьютерное моделирование поможет обеспечить требуемый уровень шума, создаваемого потоками жидкости, например, на производствах нефтегазовой отрасли или аэродинамического шума, создаваемого летательными аппаратами.

Многообразие возможностей специализированного программного обеспечения и компетенции инженеров компании АО «ЦИФРА» позволяют решать широкий спектр инженерных задачи гидро- и аэроакустики. Это определение акустического давления и уровня шума при обтекании различных объектов, полостей, углублений, выступов, при истечениях из сопел, в пропеллерах, вентиляторах, турбинах, в элементах вентиляции и арматуры. 

Список использованных источников

1. Ansys© Fluent, Fluent Theory Guide, Chapter 11 Aerodynamically Generated Noise, ANSYS, Inc.
2. Dai X., Jing X., Sun X. Flow-excited acoustic resonance of a Helmholtz resonator: Discrete vortex model compared to expreriments // Physics of Fluids. –2015. –Т. 27. – №5.
3. Lighthill M.J. On sound generated aerodynamically I. General theory // Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 211, No. 1107, March 1952. pp. 564–587.
4. Ansys© Fluent, Fluent Theory Guide, 11.2.1. The Ffowcs Williams and Hawkings Model, ANSYS, Inc.
5. Lockard D., Khorrami M., Li F. High resolution calculation of a simplified landing gear //10th AIAA/CEAS Aeroacoustics Conference. – 2004. – С. 2887.
6. Ansys© Fluent, Fluent Theory Guide, 11.2.2.Wave Equation Model, ANSYS, Inc.
7. Ansys© Fluent, Fluent Theory Guide, 11.2.3. Broadband Noise Source Models, ANSYS, Inc.

Изображение заголовка: Artturi Jalli на Unsplash